Physics and Astronomy, University of Kent
In this lecture we will explore the Doppler effect from a relativistic perspective and derive an expression for the wavelength shift of light due to relative motion between the source and a receiver. This has some important applications in cosmology, particularly related to the cosmological red-shift.
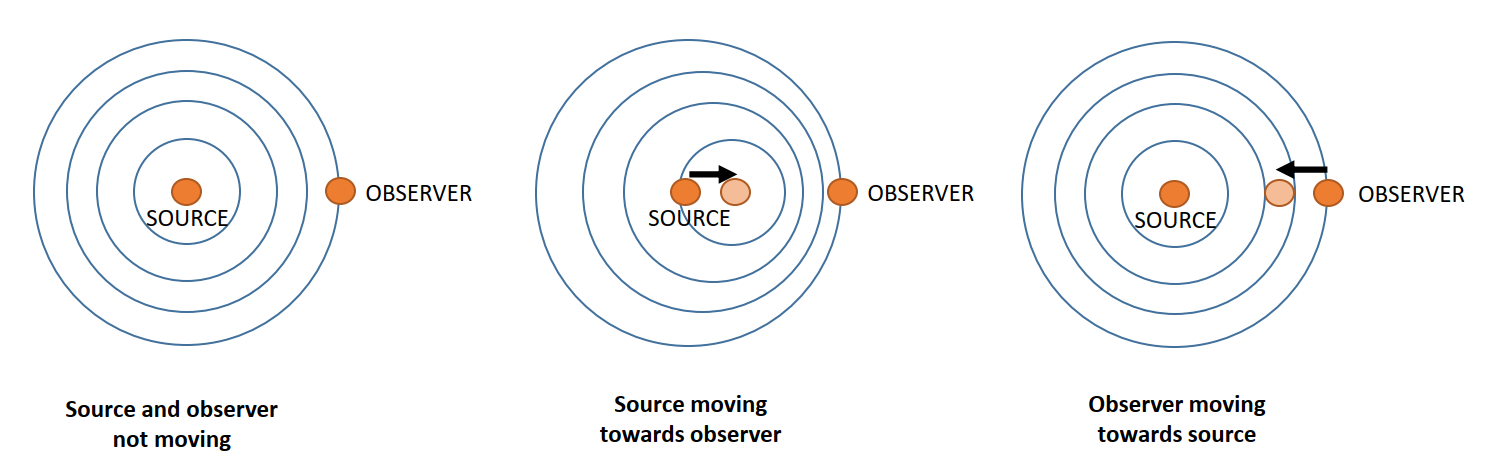
We are familiar with the Doppler effect for sound waves in everyday experience - it is the effect that causes the pitch of the noise from a car to be higher as it comes towards you, and lower as it moves away.
The explanation for this is intuitively simple when we consider that sound is a wave, travelling through air. If we are stationary (with respect to the air), then for sound waves generated by the car moving towards us the crests of the waves are closer together than they otherwise would be, and further apart when it is moving away. Closer wave crests means a higher frequency or pitch. This is illustrated in Figure 1.

Similarly, if we were moving through the air towards the car, the crests of the waves would appear closer together, giving a higher frequency, while if we were moving away, the waves would be further apart, giving a lower frequency.
To express this mathematically, consider a source of sound, generating waves such that a crest is created every \(\Delta t\) seconds. The waves travel at a velocity \(v\). If the source is moving towards an observer at velocity \(u\), then it will move a distance \(\Delta x = u \Delta t\) between the creation of each wave crest. So the next crest will have to travel a distance of \(u\Delta t\) less to reach the observer than if the source was non-moving. Since wave crests are travelling at \(v\), this means the next crest will arrive a time \(u\Delta t / v\) earlier than it otherwise would have.
So, if we call the time difference between each peak as measured by the observer \(\Delta t'\), then: \[\Delta t' = \Delta t -u \Delta t /v = \Delta t(1-u/v)\]
Now if we remember that the frequency of a wave is the inverse of the period, \(f = 1 / \Delta T\), and we label the frequency seen by the observer as \(f_{obs} = 1/ \Delta t'\) and the frequency sent by the source as \(f_{source} = 1/ \Delta t\), then we have:
\[\boxed{f_{obs} = \frac{1}{1-u/v}f_{source}}\] A similar argument shows that, if the observer is moving towards the source with velocity \(u\), \[\boxed{f_{obs} = \bigg(1+\frac{u}{v}\bigg)f_{source}}\]
These are the equations for the non-relativistic Doppler effect.
When dealing with light, we no longer have a medium that the source and the observer can move relative to. So it can only be the velocity of the source relative to the observer than can matter.
The correct equation for the relativistic Doppler effect is:
\[f_{obs} = \sqrt{\frac{1+u/c}{1-u/c}}f_{source}\] where \(u\) is velocity of the source relative to the observer.
To derive the relativistic Doppler effect equation, we will work in the reference frame of the observer. The source is therefore moving at velocity \(u\). If we think back to our equation for the observed time spacing between peaks arriving at the observer: \[\Delta t' = \Delta t(1-u/v)\] then we need to make two changes to accommodate working with light. The first is that the velocity, \(v\), is now the velocity of light, \(c\). The second is that, since the observer sees the source in motion, we need to allow for time dilation. We therefore have \[\Delta t' = \gamma (1-u/c)\Delta t.\] That’s all the physics we need, so now we expand out the \(\gamma\) term to obtain: \[\begin{aligned} \Delta t' &= \frac{1-u/c}{\sqrt{1-u^2/c^2}}\Delta t \\ &= \sqrt{\frac{(1-u/c)^2}{(1+u/c)(1-u/c)}} \Delta t \\ & = \sqrt{\frac{1-u/c}{1+u/c} }\Delta t . \end{aligned}\] Frequency is \(1/\Delta t\) and so, we obtain \[\boxed{f_{obs} = \sqrt{\frac{1+u/c}{1-u/c}}f_{source}}\] We derived this for the case that the source was moving towards the observer with velocity \(u\). If the source is moving away, we need to use \(-u\), so that \(1+u/c\) becomes \(1-u/c\) and vice-versa.
Notice something else critical here. \(u\) is the velocity of the source relative to the observer. Unlike for sound, where we cared about the velocity of both the source and the observer relative to the air, with light we only care about the relative velocity between the source and the observer. That is to say, we don’t need to derive a second equation to tell us what happens when the observer is in motion. So in some ways, the relativistic Doppler Effect is simpler!
In the cosmology section of this module, you will learn about the expansion of the universe being measured by the red shift. The idea is that if we look at wavelength spectra of light coming from stars, we see that there are lines at wavelengths corresponding to certain atomic transitions. The wavelengths that these lines should appear at are well-known from studies here on Earth. When we look at the stars, we notice that the positions of these lines appear to be shifted in wavelength. This is due to the relativistic Doppler effect, telling us that the stars are moving relative to us. (In fact they are almost always moving away, but that is another discussion).
As an example, consider measuring the spectrum from a star. We know that there should be a highly characteristic dark line in the spectrum at a wavelength of \(479.8 \, \mathrm{nm}\), which is due to the presence of hydrogen (called the H-alpha line). However, when we observe the star we instead see the line at \(537.4 \, \mathrm{nm}\). How fast must the star be moving?
First we need to remember that \(\lambda = c/f\) where \(\lambda\) is wavelength and \(f\) is frequency. So if we rewrite the Doppler equation in terms of wavelength, we have: \[\begin{aligned} \lambda_{obs}/c &= \sqrt{\frac{1-u/c}{1+u/c}}\lambda_{source}/c \\ \lambda_{obs} &= \sqrt{\frac{1-u/c}{1+u/c}}\lambda_{source} \end{aligned}\]
A bit of algebra gives us:
\[\boxed{u/c = \frac{\lambda_{source}^2 -\lambda_{obs}^2}{\lambda_{source}^2 +\lambda_{obs}^2}}\] which is useful to remember. If we can substitute in our known source wavelength (\(\lambda_{source} = 479.8 \, \mathrm{nm}\)) and our wavelength observed here on Earth (\(\lambda_{obs} = 537.4 \, \mathrm{ nm}\)), we find that the star is moving with a velocity of \[u = -0.11c\]
Notice that the observed wavelength was longer than the source wavelength. Longer wavelengths are towards the red end of the visible spectrum, and so we call this redshift. Redshifted light implies that the source is moving away from us. Hence we had a negative value for \(u\) (remember that we derived this equation for a source moving towards the observer with velocity \(u\)). Therefore the star is moving away at a velocity of \(0.11c\).