Physics and Astronomy, University of Kent
We will now looks at some deeper aspects of special relativity, studying the breakdown in our ideas of absolute simultaneity. Some non-examinable ideas are also covered, including the spacetime interval, a quantity which can be considered absolute in the sense that it does not change under a Lorentz transformation. This is include here for interest, you will study it in more detail in later courses.
The ladder "paradox" is a classic situation in special relativity. If you understand the ladder paradox you are a good way to understanding the key ideas of the theory.
A farmer is standing next to his shed. He would like to put his ladder inside the shed, but he has a problem. The shed is 2 m in length while the ladder is 4 m long. Luckily, he has studied PH304, and he has an idea. He realises that if he moves the ladder at a velocity of \(\sqrt{3}c/2\), he will have a gamma factor of \(\gamma = 2\). The ladder will then be length contracted, in the frame of the farmer and the non-moving shed, by a factor of 2, making it 2 m in length and just able to fit inside the shed.
Of course, it won’t be in the shed for very long before it crashes through the other side. However, in a second stroke of luck, the shed has two sets of doors, front and back. The ladder will enter the front door, which he can then quickly close, momentarily trapping the ladder inside. To prevent any damage to his shed doors, he will then immediately open the back door, allowing the ladder to pass through and carry on its way at \(\sqrt{3}c/2\).
Leaving aside questions of how he accelerates the ladder, or opens and closes the doors so fast, does this work?
From the rest frame of the shed, it looks like it will indeed work. The difficulty comes when we consider things from the rest frame of the ladder (the ladder’s point of view). From this frame it is the shed that it is moving, and so length contracted by a factor of 2. So now the shed is only 1 m in length, while the ladder maintains its length of 4 m in its rest frame. So in the rest frame of the ladder, things are even worse than they were to start with!
How is this paradox resolved? The answer is that the closing of the front and back doors of the shed are events separated in space. This means that while they are simultaneous for the farmer/shed, they are not simultaneous for the ladder. The ladder will see the back door open before the front door closes, and so it will never be entirely within the shed.
There is a problem on Worksheet 2 in which you will work through this in more detail.
It is clear from the Lorentz transform for time: \[t' = \gamma(t - ux/c^2),\]
that time is measured differently for observers moving in different inertial frames. A consequence of this, which may not be immediately apparent, is that two events which are separated in space, and which one observer considers to occur at the same time (i.e. they are simultaneous), will not be simultaneous in a different inertial frame. Indeed, in some circumstances it may even be that the two observers do not even agree on the ordering of the events. It is often the failure to fully appreciate the breakdown of absolute simultaneity which can leads to difficulties in our understanding and apparent "paradoxes".
Consider two events occurring, events 1 and 2. They occur at two positions along the x-axis, \(x_1\) and \(x_2\), at times \(t_1\) and \(t_2\), as measured by an observer in reference frame \(S\). Let’s say that in reference frame \(S\) they are simultaneous, that is \(t_1 = t_2\) , and let’s call this time \(t_1 = t_2 = 0\).
Now consider a second reference frame, \(S'\) moving at \(u\). From the Lorentz transformations, we can calculate the times of the events in \(S'\): \[t_1' =\gamma(t_1 - ux_1/c^2) = \gamma(-ux_1/c^2)\] and \[t_2' =\gamma(t_2 - ux_2/c^2) = \gamma(-ux_2/c^2)\] It’s immediately obvious that \(t'_1 \neq t'_2\) unless \(x_1 = x_2\). That is to say that events which are separated in space and are simultaneous in \(S\) are not simultaneous in any other frame \(S'\). We can also see that the order of \(t_1'\) and \(t_2'\) is not fixed, and depends on the values of \(x_1\) and \(x_2\).
The twin paradox is less illustrative of the principles of special relativity, but is nevertheless important for other reasons. It is illustrated in Figure 1.
An astronaut sets out from Earth at a speed \(v\), which is some appreciable fraction of the speed of light. She travels for some distance, turns around and comes back. The question is, will her clock agree with the clock of her twin sister who has stayed on Earth? Or to put it another way, will they have aged differently?
From the point of view of the twin on Earth, the astronaut has been moving, and so time should have been running slower for the astronaut; while the astronaut measures a time \(t\) on her clock, the twin at home measures a time \(\gamma t\) on her clock. So when the astronaut arrives back at Earth, she will have aged less and be younger than the twin who stayed behind. So far, so good.
But now let’s look at it from the point of view of the astronaut. In her rest frame, she says that it is actually the Earth that moves away and then comes back. So from her point of view, everything is reversed, and she says that it will be the twin who stayed on Earth who will be the younger.

Clearly both can’t be correct; when they stand next to each other and compare their clocks, they cannot both be the slow ones. So what has happened?
To find the answer we return to the first postulate, which says that the laws of physics are the same in all inertial frames. But the astronaut was not in an inertial frame, she would have felt the acceleration as she left Earth, the deceleration at the mid-way point and acceleration back towards Earth and then a final deceleration as she arrived.
In principle we can ignore the accelerations at Earth - we could always synchronise clocks in a flypast. But there is no way to avoid the acceleration at the mid-way point. One way of thinking about it is that, at the time she turned around, the astronaut jumped between two different inertial frames travelling in opposite directions.
So who is correct? The answer is the twin who stayed on Earth. Since she stayed in an inertial frame at all times, it is perfectly valid for her to calculate everything using the Lorentz transformations. For the astronaut, it is not.
This goes to the heart of the matter of symmetry in special relativity. Two observers moving relative to each other both say that the other’s clock is running slow. This is not a paradox, because the clocks are spatially separated at all times (except for time \(t=0\) for which \(t'=0\) so they both still agree.) In order to bring the clocks together, so we can look at them side by side, we require an acceleration, in which case we change the calculation!
We can represent objects in space and time by a diagram called a spacetime diagram, shown in Figure 2. Since there are three spatial dimensions (\(x\),\(y\),\(z\)) plus time \(t\), a true spacetime diagram would need to be four dimensional! However, since we are normally only interested in the position along the axis of motion, which we label as \(x\), we can draw useful spacetime diagrams only involving \(x\) and \(t\).
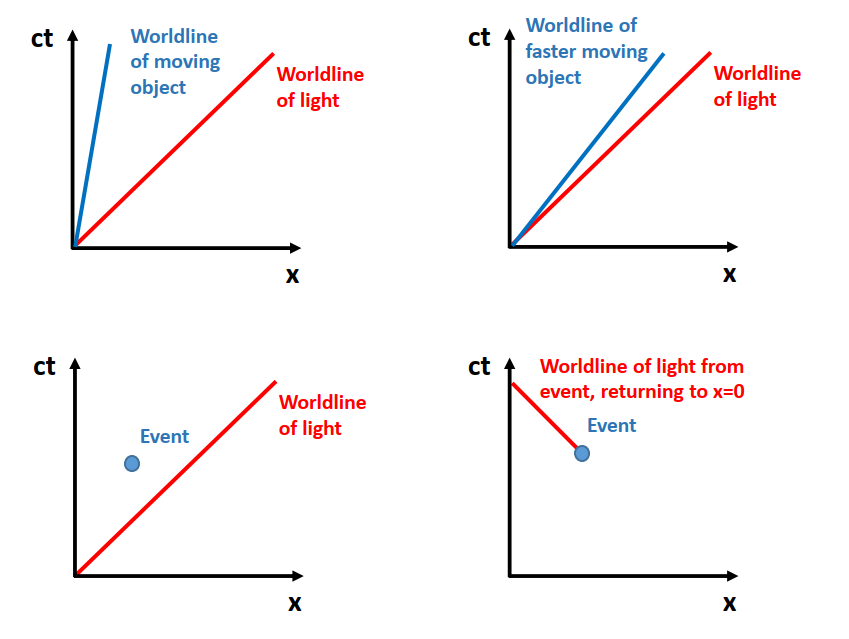
Individual events can be plotted, and the path an object takes through a spacetime diagram is called its worldline. Notice a couple of things. Firstly, we plot \(ct\) rather than \(t\). This is so that the worldline of light is at 45 degrees. Secondly, \(ct\) is plotted on the y-axis and \(x\) on the x-axis. This may be slightly counter-intuitive, as we are used to thinking of \(t\) as the independent variable going on the x-axis, but it quickly becomes natural with practice. Try to think of \(x\) and \(ct\) as just two different co-ordinates in spacetime.
We speak about a quantity being Lorentz Invariant if it does not change when we switch between reference frames. Note that this is a very different concept from a conserved quantity (such as momentum) which doesn’t change in time.
Clearly \(x\) and \(t\) are not Lorentz invariant, since the Lorentz transformations tell us that they change between reference frames. But we can ask whether there is some other invariant quantity which is a combination of \(x\) and \(t\).
An analogy which may be useful is to think of the points on a circumference of a circle. As we move around the circle, which we can think of as a rotation, our x and y co-ordinates change. However, the radius of the circle (our distance from the centre) is invariant, given simply by \(r^2 = x^2 + y^2\).
There is something similar we can calculate for space and time under Lorentz transformations. While space and time (\(x\) and \(t\)) change, there is a value that we can calculate which is invariant. This invariant is called the spacetime interval or spacetime distance and is given by:
\[(\Delta s)^2 = (\Delta x)^2 - (c\Delta t)^2\]
This looks a little similar to our circle invariant, although with some obvious differences. In particular, we notice that it is \(- (c\Delta t)^2\) and not \(+(c\Delta t)^2\). This means that the spacetime interval can be negative or positive, depending on whether \((c\Delta t)^2\) is smaller or bigger than \((\Delta x)^2\). By analogy to the circle we can think of a Lorentz transformation being something like a rotation in spacetime, with the proviso that the geometry of spacetime is a little different from the Euclidean geometry we are used to.
Whether the right-hand-side is positive or negative (or 0) has a very important physical meaning. First lets consider the very special case of \((\Delta s)^2\) = 0. This means that \[\begin{aligned} (\Delta x)^2 &= (c \Delta t)^2 \\\Delta x&=c \Delta t \end{aligned}\]
If the distance travelled is \(c\) times the time, then the velocity is obviously \(c\). We call this lightlike or ‘null’.
If two events are separated by \((\Delta s)^2 > 0\) then this means than the distance between them is larger than \(c \Delta t\). We call this a spacelike interval. It means that there is some reference frame where the two events are simultaneous, in which case they will be separated by a distance of \(\Delta d\) (but only in that special reference frame). There can be no causal link between the two events, because even a signal travelling at the speed of light couldn’t have covered the distance in time. Therefore a change in the order of the events does not violate causality - there can be no mixing of cause and effect.
If two events are separated by \((\Delta s)^2 < 0\) then we call this interval timelike. There is no reference frame where these two events are simultaneous, but there is a reference frame where they occur at the same place at different times, with a time difference of \(t=\sqrt{-\Delta s^2)}/c\). All observers must agree on the order in which the two events occurred. This is critical because, if two events are timelike separated, then there could have been a causal link between them, and no-one can observe an effect happening before its cause!
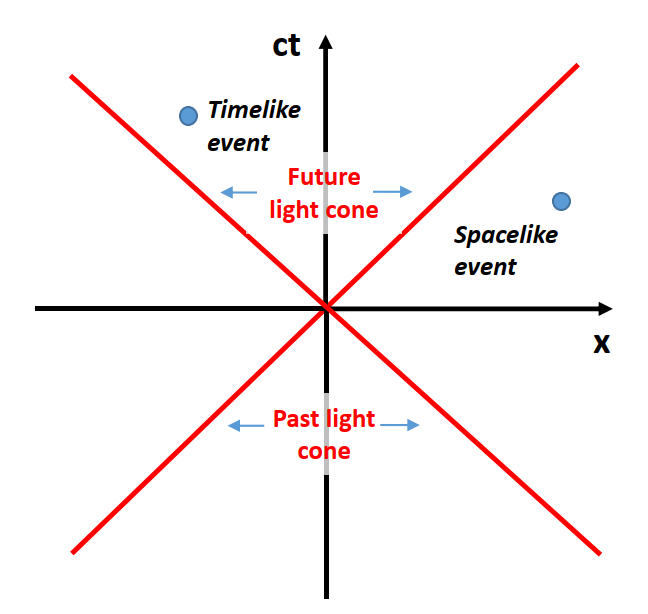
A nice way to visualise spacelike and timelike spacetime distance is using our spacetime diagrams. If we place an observer at the origin and draw lines for \(x=ct\) and \(x=-ct\) we obtain what are known as ‘light-cones’, shown in Figure 3. For positive times this is the ‘future light cone’ and for negative times it is the ‘past light cone’. Only events in your past light cone can influence you now, and you can only influence events in your future light cone. Signals from events which are outside your past light cone (events which are spacelike separated from you) cannot possibly have reached you yet, and you cannot possibly send a signal to events outside your future light cone.
Note that the spacetime interval will not be on the exam (although you may find it in past papers) - This is now covered, along with other invariants, as part of the Stage 2 relativity course.