In 1905 Albert Einstein published his classic paper "On the Electrodynamics of Moving Bodies". This was the birth of special relativity, although it was not given that name at the time. By the end of this course you should be able to follow much of the kinematical part of this paper (or at least the English translation of it - see the link on Moodle).

Einstein’s ideas were quickly built on by Hermann Minkowski and others and - despite special relativity’s apparently counter-intuitive predictions - it almost immediately gained acceptance as the correct physical theory describing the relationship between space and time. Together with the later theory of general relativity, which we will not study in this course, it has since been experimentally verified to an extraordinary degree of accuracy.

We will follow a quasi-historical approach to learning the theory, beginning in this lecture by exploring the classical notions of relativity and the Galilean transformations between reference frames. You need to be very comfortable dealing with transformations between reference frames before moving on. We will then discover a fundamental incompatibility between these ideas and the electromagnetic theory which was developed in the mid-18th century. Attempts to resolve this discrepancy by introducing the idea of the ‘ether’ failed, leading us in the next lecture to the derivation of the Lorentz transformations, to the discovery of time dilation and length contraction, and to a breakdown in our notions of absolute simultaneity.

In later lectures we will encounter the more modern idea of ‘spacetime’ and the invariant spacetime interval. We will discover that we must modify our definitions of momentum and energy, and we will show that there is an equivalence between energy and mass, leading to perhaps the most famous physics equation of all: \(E=mc^2\).

Frames of Reference and Events

A frame of reference can be thought of, informally, as a ‘point-of-view from which a measurement is made by an observer’. We will study how measurements made by observers in different reference frames are related to one another. The measurements will be, initially, of the locations and times at which events occur, and the spatial and time intervals between the events.

We will deal mostly with non-accelerating reference frames, i.e. observers who are not accelerating. These non-accelerating reference frames are called inertial reference frames.

We can tell we are in an inertial reference frame because we don’t feel ‘pseudo forces’. For example, think of when you are in an accelerating car, and you seem to feel a force pushing you back onto the seat (sometimes known as ‘G-forces’). In inertial reference frames we don’t have these extra forces, the simple laws of mechanics hold; whenever we see an acceleration we also see a force that causes that acceleration (\(F=ma\)).

A person in an inertial frame of reference, i.e. moving at a constant speed, cannot tell that they are moving except by reference to other objects. That is, no experiment can tell you what your absolute velocity (or speed) is, only your velocity or speed relative to something else. For example, if you are standing on the ground and looking at a train going past, you will measure it to have a speed of \(u\) in a certain direction. But from the point of view (the frame of reference) of someone on the train, they are not moving, and it is the Earth and you moving at a speed of \(-u\) relative to them. This is the Principle of Relativity, which predates the theory of special relativity by several hundred years.

It’s also useful to define what we mean by a ‘rest frame’ at this point.

Transformation between Inertial Reference Frames

If we measure the co-ordinates of an event in two different reference frames, we can convert between those measurements using transformations.

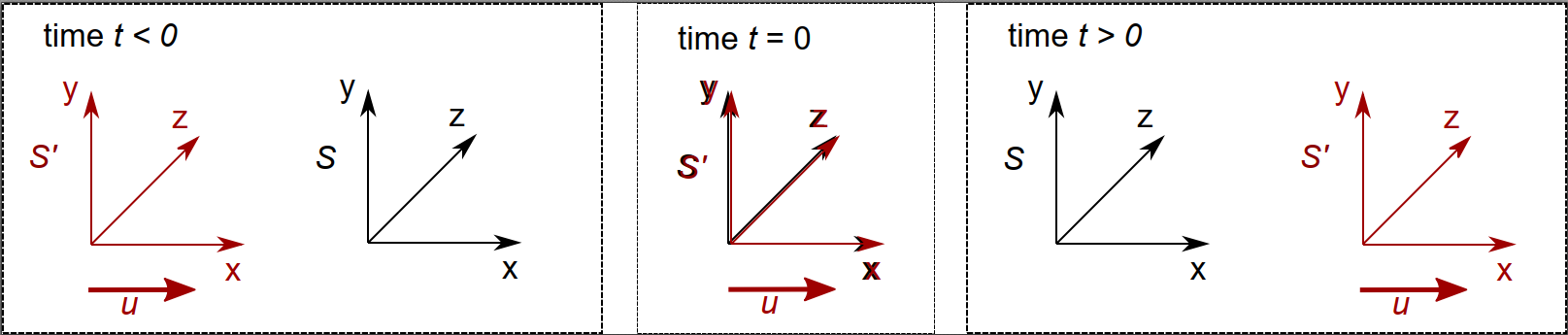
Let’s return to our example of a train passing by someone standing by the side of the tracks. For the driver and the observer we will define two reference frames and co-ordinate systems. We could define these in all sorts of ways, and of course it wouldn’t change the physics, but there is particular way of defining things which makes the problems we will encounter as simple as possible.

The scheme we will use is shown in Figure 1.

We call the reference frames, and their associated co-ordinate systems, \(S\) for the observer and \(S’\) (which we say ‘S prime‘) for the driver. We will measure the location and time at which events occur from both reference frames. For the location of the event, we will use standard Cartesian co-ordinate systems:

• \(x\), \(y\), and \(z\) for the driver’s frame of reference, \(S\);

• \(x’\), \(y’\) and \(z’\) for the trackside observer’s frame, \(S’\).

We will align the two co-ordinate frames, so that \(x\) is parallel with \(x'\) and so on. The motion of the train, and hence the \(S'\) reference frame, is along the x-axis of frame \(S\), in the positive direction, with speed \(u\).

We will also have co-ordinates for the time of the event, which we will call \(t\) and \(t'\) for the two reference frames. Again, for simplicity, we’ll set time \(t=0\) and \(t'=0\) at the point where the train passes the trackside observer. In Newtonian physics, everyone experiences time the same, so for now we have that \(t=t'\) at all times anyway, but later on we will find something quite different.

Now let’s imagine some event occurring, the driver sneezing for example. Recall that an event is something that can be described by space and time co-ordinates - it happens at a certain place at a certain time. An event does not belong to a reference frame; it can be measured or observed from different reference frames.

To define the co-ordinates of this event we need to know its location in space and time (i.e. where and when it happened). In the co-ordinate system of the train driver, that is straightforward. For simplicity we will say the driver is at \((x',y',z') = (0,0,0)\), i.e. at the origin of his reference frame, which we call \(S'\).

Now, what is the spatial location and time of the sneeze (the ‘event’) from the point of view (i.e. in the rest frame) of the observer by the side of the track?

• The train is moving past at speed \(u\), so after an amount of time \(t\) the car will have moved \(ut\) along the x-axis.

• So, the \(x\) co-ordinate of the event will simply be \(x' + ut\).

• The train has not moved along the y and the z-axes, and so \(y=y'\) and \(z=z'\).

• Time is the the same for everyone, \(t=t'\).

We can now write down the full set of equations to transform the co-ordinates of event measured in frame \(S\) into the co-ordinates measured in frame \(S'\) and vice versa. These are known as the Galilean transformations.

Notice that when going from \(S\) to \(S'\) we have a \(-ut\) rather than a \(+ut'\) or \(+ut\). This is because, from the point of view of the train driver, the observer is moving backwards along the x-axis. Otherwise the equations are the same. It is a requirement of the principle of relativity that the transformations going from \(S\) to \(S'\) are the same as those going from \(S\) to \(S'\) (except for the sign change).

Now let’s imagine that the driver of the train leans out of the window and throws a ball along the x-axis, with a speed \(v'\) relative to himself and the train. How fast does the observer think the ball is moving (\(v\))? You can probably guess straight away that she sees the speed of the ball added to the speed of the train, i.e. \(v=v'+u\), where we remember that \(u\) is the speed of the train relative to the track-side observer. Thinking of this in terms of the speeds along the x, y and z axes, we have the Galilean velocity (speed) transformations:

These can also be obtained simply by differentiating the Galilean transforms with respect to time, which is left a simple exercise.

The Speed of Light

It has been known since the experiments of Ole Römer in the 17th century that light travels with a finite speed. Successive measurements over the years have succeeded in fixing the value in a vacuum, known as \(c\), at approximately \(3\times10^8\) m s⁻¹. But what is this relative to?

As an analogy, we know that sound travels in air at approximately \(300\) m s⁻¹, and much faster in other, denser materials. Sound is a wave in a medium. So it is reasonably that the velocity is relative to the medium (e.g. air,) and indeed this is what we find experimentally. The speed of sound does not depend on the speed of the source of the sound, and so if the source is travelling through the air faster than the speed of sound, it’s possible for it to overtake sound - this is the effect responsible for the sonic boom heard from supersonic jets. Conversely, inside a sealed plane, the air is moving along with the plane, so sound will continue to travel at \(300\) m s⁻¹ relative to the passengers.

Unlike for sound, where we have an obvious medium supporting the sound wave, it is not clear what light is a wave in , since light travels through a vacuum.

In 1862, James Clark Maxwell discovered that light is in fact an electromagnetic wave - a wave in electric and magnetic fields. He showed that the speed of light can be predicted from the fundamental equations describing electricity and magnetism, known as Maxwell’s Equations. Crucially, when deriving the wave equation, no account is taken of relative velocities, and we don’t define a carrying medium. Maxwell’s equations, unlike Newton’s laws, do not appear to remain the same when moving between reference frames using the Galilean transformations. So it would be possible to determine we are moving by making measurements of electrical and magnetic phenomena. In particular, our ‘absolute speed’ could be determined simply by measuring the speed of light in our reference frame. For example, if we measure the speed of light to be \(c + 10\) m s⁻¹ that means we are moving at \(10\) m s⁻¹ relative to this absolute reference frame.

The Ether

If an absolute reference frame were to exist (we will soon see it does not), what form would it take? One idea was that there is some medium called the ether which fills the universe, and it would be this is the material in which light waves travel. The ether, if it existed, would allow light waves to travel at very high speed but also seems to be undetectable - we cannot feel it and it seems not to slow objects down that are moving through it. It does, however, apparently solve the problem of the relativity of the speed of light: the speed of light is fixed relative to the ether.

Unfortunately, as we will now see, the idea of the ether doesn’t work, or rather, it contradicts the results of experiments in ways that are seemingly impossible to resolve.

Experiments to Detect the Ether

In the second half of the nineteenth century, a number of experiments were performed with the intention to detect the presence of the ether, or more specifically our motion through it. We shall discuss only one, the Michelson-Morley experiment, as it is both simple to understand and definitive.

The assumption behind the experiment is that, if the Earth is moving relative to the ether, this would mean that we would measure different speeds of light depending on the relative speed of the Earth. If we measure the speed of light along the direction of the Earth’s motion, we should get a different value than if we measure the speed of light moving perpendicular to the Earth’s motion. Furthermore, since the Earth is in orbit around the Sun, we would expect that the speed of the Earth relative to the ether changes throughout the year. If at one point in the year the Earth is moving at \(v\, \rm m/s\), then sixth months later, on the other side of the orbit, it will be moving at \(-v\,\ rm m/s\). So if we measure the speed of light relative to the Earth, we should obtain different values.

This was the idea behind the Michelson-Morley experiment. Clearly it is quite difficult to measure the speed of light because it is so fast. However, it can be done (and could be even in 1895) with a technique called interferometry, as illustrated in Figure 2. This idea is to split light into two arms of the interferometer. Light bounces of a mirror in each arm and is then recombined. Light is a wave and so, providing the lengths of the two arms are the same, we see interference effects, giving rise to light and dark fringes. These fringes are very sensitive to the travel time of the light (either due to a change in its speed or a change in the length of one of the arms).

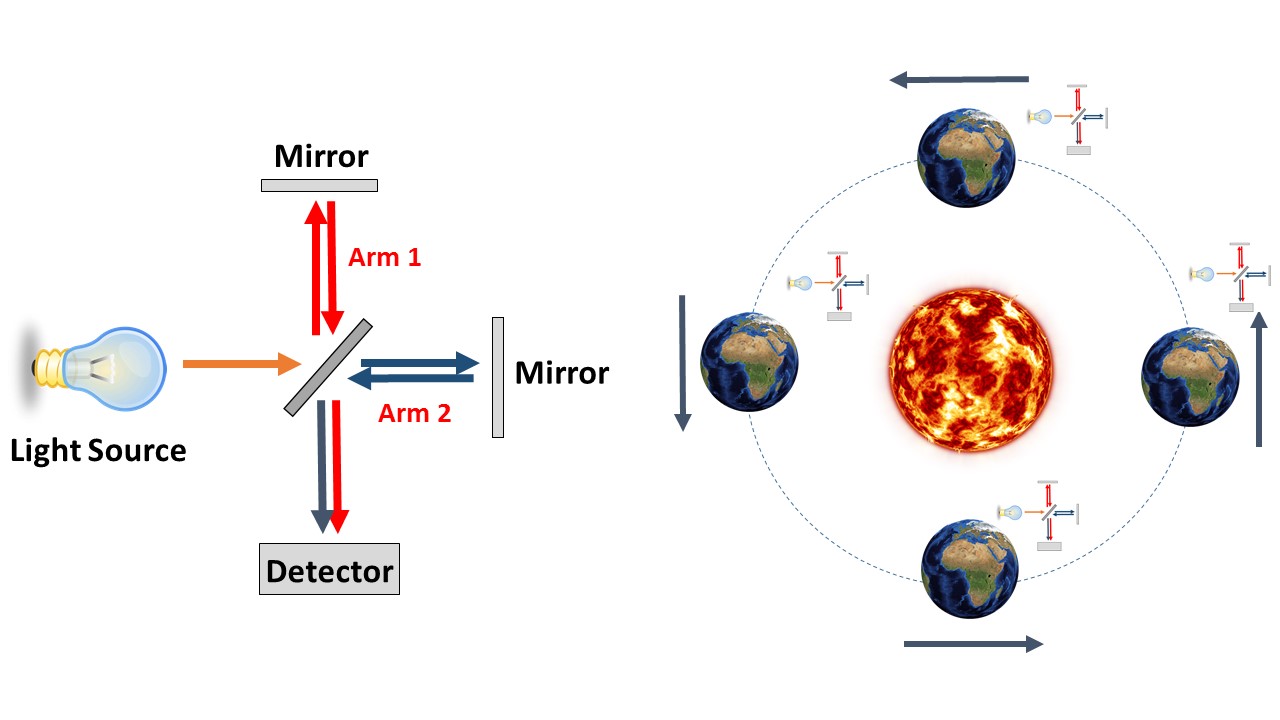
The idea then is to set up the interferometer and observe the fringes. Then, rotate the interferometer by 90 degrees and look at the fringes again. If the speed of light is different in the two directions, the fringes will change. To avoid the possibility that the experiment happened to be carried out at the point in the Earth’s orbit where it had zero speed relative to the ether, it can be repeated six months later.

No difference in the speed of light was measured. Regardless of which way around the interferometer was, or what time of year the measurements were made, the speed of light was always measured to be the same. To put it another way, light does not follow the rules for velocity transformations, in every reference frame light appears to travel at \(c\)!

How could this be explained? One possibility was that the ether is somehow dragged along with the Earth on its orbit, so that the experiment was always measuring the speed of light relative to the moving ether. On practical grounds it becomes hard to explain this, and it also contradicts other observations (such as stellar aberration, which we will not discuss).

A much more elegant solution, dispensing with the idea of the ether altogether, was presented in 1905 by Albert Einstein: the special theory of relativity.