Nuclear Physics Section 4 - The Shell Model

In this section we move on from deuteron to consider more complex nuclei and develop the shell model. Now we have no hope of solving the Schrödinger equation exactly and will need to make some simplifying approximations.

Evidence for the Shell Model

We can now extend our treatment to other nuclei and postulate a shell model. This is a conceptually similar idea to the shell model for atoms. There is certainly ample evidence for a shell model for nuclei.

Firstly, it is found that nuclei with even number of protons and neutrons are more stable than those with odd numbers (this was captured in our pairing term for the SEMF). This suggests that some type of pairing is going on, similar to the idea of having two electrons per energy level in an atom. There are certain magic numbers of protons and neutrons which seem to produce very stable nuclei with high natural abundances. These magic numbers are: 2, 8, 20, 28, 50, 82 and 126. Nuclei which have these numbers of both N and Z are ‘doubly magic’ and even more stable.

This seems to suggest some sort of ‘filling’ of shells, again analogous to filling electron shells in an atom. The neutron cross-section, the probability of these nuclei absorbing a further neutron, is also lower than for other nuclei.

The liquid drop model does not explain these features, and the binding energy of magic number nuclei is poorly modelled by the semi-empirical mass formula.

The Shell Model

The huge simplification here is that, rather than trying to model individual interactions between individual nucleons, we are assuming that each nucleon sees an average ‘net’ potential due to all the other nucleons. This net potential is then the potential in the Schrödinger equation. However, as when we modelled the deuteron, we have the problem that we don’t know exactly what this potential is.

Some experimentation can determined that a good guess for the potential is to assume that is spherically symmetric and takes the form: \[V(r) = - \frac{V_0}{1 + \exp \frac{r-R}{a}} \label{eqn:fermiPot}\] where \(V_0\) is a constant, \(r\) is the radial co-ordinate and \(R\) and \(a\) are constants. You may remember that we studied this equation in Workshop 1 in a slightly different context, so you will know that \(R\) is the radius of the potential and \(a\) is related to the skin thickness. We can choose \(R = r_0A^{1/3}\) and we determined in the worksheet that a value of \(a\approx 0.5\) fm gives a skin thickness that matches experiment. The potential energy (well depth) \(V_0\) is again an unknown, so we would have to try different values until we reproduce experimental binding energies, it turns out \(V_0 = 50\) MeV gives the best results.

The solution to this spherical potential will then have the form: \[\Psi = R_{nl}Y_{lm_l}(\theta,\phi)\]

As before, the \(R\) is a radial component and the \(Y\) is the angular component and these solutions are separable. The solutions for \(R\) are spherical Bessel functions and the solutions for \(Y\) are spherical harmonics. The solutions are parameterised by the principal quantum number (\(n\)), the angular momentum quantum number (\(l\)) and the magnetic quantum number (\(m_l\)). Each solution has an an associated energy, \(E_{nl}\) which depends on \(n\) and \(l\) but not on \(m_l\). We say that solutions with different \(m_l\) are degenerate.

The degeneracy of each level, i.e. the number of nucleons that can have each energy level, is \(2(2l + 1)\), where the initial factor of two allows for the two \(m_s\) spin states and the \(2l + 1\) allows for the different \(m_l\) states.

The important thing to realise that protons and neutrons fill up their own shells. Protons and neutrons are not identical particles and so the Pauli exclusion principle doesn’t apply between a proton and a neutron.

Comparison with Atomic Energy Levels

If we compare with the atomic shell mode, we can also identify two other important difference:

We label the levels with a number and a letter, the letter being the \(s\), \(p\), \(d\), \(f\), ... of the spectroscopic notation, representing \(l\). So for example, \(1s\), \(2\)p etc. The difference with similar looking notation for atomic energy levels is that the number does not indicate the principal quantum number, but the \(n\)th state of that \(l\). For example \(2p\) is the second \(p\) (\(l = 1\)) state. So we see states such as \(1f\) which would not occur in atomic physics.

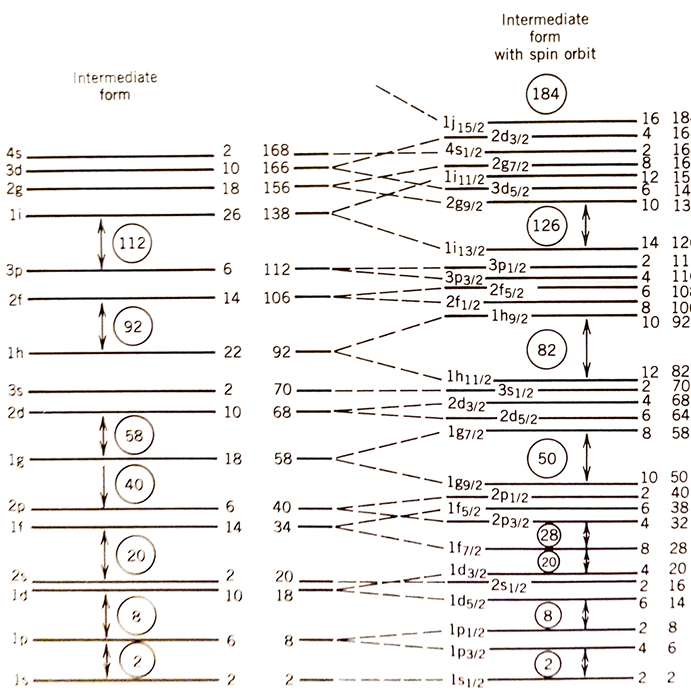
Like in atomic physics, the energy-ordering of the levels is not as nice as we might have hoped, as shown in Table 1. (There is no need to memorise the order, I would give you this in an exam, but you would need to known how to work out the degeneracy.)

Shell filling predicted by a simple shell model
	1s	1p	1d	2s	1f	2p	1g	2d	3s
Degeneracy, \(2(2l +1)\)	2	6	10	2	14	6	18	10	2
Running total	2	8	18	20	34	40	58	68	70

We would expect nuclei with full shells to be particularly stable, i.e. these should be the nuclei corresponding to magic numbers of protons and neutrons. Unfortunately, these totals do not match the observed magic numbers, so we have not managed to accurately predict shell-filling effects. Tweaking the potential does not fix this problem.

Spin-Orbit Coupling

As we discussed previously, the total angular momentum for a nucleus is a combination of the orbital angular momentum and spin of its constituents. An effect called ‘spin-orbit’ coupling requires a modification to the potential.

The modified potential is: \[V' = V_{Fermi}(r) - V_{SO}(r)(l \cdot s) \label{eqn:SOPot}\] where we have labelled the original potential from Equation [eqn:fermiPot] as \(V_{Fermi}\). The form of \(V_{SO}\) is not so critical for the magic numbers, it is the \(l \cdot s\) term which causes a re-ordering of the energy levels.

This new term is attractive when \(l\) and \(s\) are parallel and repulsive when they are anti-parallel (we look at this in more detail later). To put it another way, states for which \(l\) and \(s\) are anti-parallel are more tightly bound.

We label states by their total angular momentum, \(\vec{J} = \vec{L} + \vec{S}\). This means that the quantum number \(j\) can either be \(|l - s|\) or \(l + s\). (This is derived below).

The simplest way to see what happens is via an example. Consider a \(1f\) state (\(l = 3\)). In this case, spin-orbit coupling could give us two possible values for the nucleus spin, we could have \(j = |l - 1/2| = 5/2\) or \(j = l + 1/2 = 7/2\). We label these states as \(1f_{5/2}\) and \(1f_{7/2}\).

Each of these states has degeneracy \(2j + 1\) (recall that \(m_j\) runs from \(-j\) to \(+j\)):

So there are 14 states in total. Before we took into account spin-orbit coupling we had \(2(2l+1) = 2(2[3]+1) = 14\) states. So, we haven’t created any more states. We have just regrouped previously degenerate states into two groups of different energies.

Calculating the energy levels of these new groups is a little messy (see Krane p124 for details), but when we do work out the new series of energy levels (Figure 1 and Table 2) we find we can reproduce the magic numbers perfectly. This is a huge vindication for the shell model and spin-orbit coupling.

Shell filling with spin-orbit coupling
	\(1s_{1/2}\)	\(1p_{3/2}\)	\(1p_{1/2}\)	\(1d_{5/2}\)	\(2s_{1/2}\)	\(1d_{3/2}\)	\(1f_{7/2}\)	\(2p_{3/2}\)	\(1f_{5/2}\)
Degeneracy [\((2j+1)\)]	2	4	2	6	2	4	8	4	6
Running Total	2	6	8	14	16	20	28	32	38

We also predict a new magic number of 184 that has not yet been observed. This ‘island of stability’ could mean super-heavy nuclei with long decay half-lives. However, they do not occur naturally and the technology to produce them artificially has not yet been developed.

Derivation of level splitting

We can check how \(\vec{L}.\vec{S}\) in Equation [eqn:SOPot] modifies the potential. Beginning with \(\vec{J} = \vec{L} + \vec{S}\), from geometry we can also say: \[J^2 = L^2 + S^2 - 2\vec{L}\cdot \vec{S}\] where \(J = |\vec{J}|\) and so on. Re-arranging: \[\vec{L}\cdot \vec{S} = 1/2(J^2 - L^2 - S^2)\]

We parameterise \(J\) with the quantum number \(j\), such that \[J^2 = j(j+1)\hbar^2\]

For the case where the \(l\) and \(s\) are aligned, we have \(J = L + S = L + 1/2\) and so: \[\begin{aligned} J_{(L+S)}^2 &= (l + 1/2)(l + 3/2)\hbar^2 \\ &=(l^2 + 2l +3/4) \hbar^2 \end{aligned}\] and so \[\begin{aligned} \vec{L} \cdot \vec{S} &= 1/2[(l^2 + 2l +3/4)\hbar^2 - l(l+1)\hbar^2 - s(s+1)\hbar^2] \\ &= 1/2[(l^2 + 2l +3/4)\hbar^2 - l(l+1)\hbar^2 - 1/2(1/2+1)\hbar^2] = (1/2)l \hbar^2 \end{aligned}\] where we have used that \(S = s(s+1)\hbar^2\) and \(L =l(l+1)\hbar^2\).

Similarly for for the anti-aligned, \(J = L - S\), case we have: \[\begin{aligned} J_{(L-S)}^2 &= (l - 1/2)(l + 3/2)\hbar^2 \\ &=(l^2 - 1/4) \hbar^2 \end{aligned}\] and then \[\begin{aligned} \vec{L} \cdot \vec{S} &= 1/2[(l^2 - 1/4)\hbar^2 - l(l+1)\hbar^2 - s(s+1)\hbar^2] \\ &= 1/2[(l^2 -1/4)\hbar^2 - (l^2+l)\hbar^2 - 3/4\hbar^2] = -(1/2)(l+1) \hbar^2 \end{aligned}\] So we can see that there is a difference in sign, as we would expect, and also a different in the magnitude. The difference in energy between the split states will therefore be proportional to: \[\begin{aligned} \Delta_{\vec{L} \cdot \vec{S}} & = (\vec{L}\cdot \vec{S})_{(L + S)} - (\vec{L}\cdot \vec{S})_{(L - S)} \\ &= (1/2) l \hbar^2 - [ -(1/2)(l + 1)\hbar^2] \\ &= (l + 1/2)\hbar^2 \end{aligned}\]

Nuclear Spin and Parity from the Shell Model

The shell model allows us to predict the spins and parities of the ground states of certain nuclei:

Even-Even nuclei have spin (i.e. total angular momentum) of 0 and parity even. This is a very simple rule to apply.

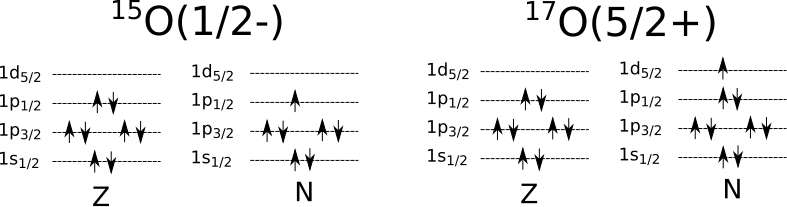
The spin and parity of on odd-even or even-odd nucleus is determined by the single unpaired nucleon. This can be either a single nucleon in a level, or a single hole in a level. For example, take \(^{15}_8O\). There are 8 protons, completely filling to the \(1p_{1/2}\) level. There is one fewer neutron, leaving the \(1p_{1/2}\) level unfilled. This is the state that determines the spin of the nucleus, \(j = 1/2\). The unpaired neutron is in the \(p\) state, which is \(l = 3\). Recall parity =\((-1)^l\), so the parity is odd. We write this state as \(^{15}_8O(1/2-)\)

For another example, take \(^{17}_8O\). Now there is a single neutron in the \(1d_{5/2}\) level. So we have spin \(j=5/2\). The unpaired neutron is in the \(d\) state, which is \(l = 2\). So now the parity is even. So the state is \(^{17}_8 O(5/2+)\). The configurations of these two isotopes of oxygen are illustrated in Figure 2.

Odd-odd nuclei have spin which is sum of the spins of last two unpaired neutrons and protons. These nuclei are rarely stable.

Remember, these last three rules only apply for nuclei which are 1 nucleon under or 1 nucleon over a full shell. They also only work reliably for nuclei in the ground state. Nevertheless, it is another strong piece of evidence that the nuclear shell model is a good one.

Predictions of the Shell Model

Spin, Parity, Pairing and Symmetry

In the previous section we saw that the shell model allows us to predict the ground state spin (\(j\)) and parities for a range of nuclei. In particular, nuclei with even numbers of both protons and neutrons (even-even nuclei) are found to have \(j=0\) and even parity. This is due to pairing effect, whereby the \(m_j\)s effectively cancel each other out, leading to no net angular momentum.

For nuclei with odd numbers of one type of nucleon (protons or neutrons), known as even-odd nuclei, we also saw that in the cases where this led to them being one short or one over filling a shell, the nuclear spin and parity was equal to the under-filled or singly-filled shell, respectively.

These pairing effects (or lack thereof) are the origin of the pairing term in the semi-empirical mass formula. Nuclei with even-even are the most stable, while stable nuclei with odd-odd configuration are very rare.

The existence of two separate shell structures (protons and neutrons) goes a good way to explaining the symmetry term in the semi-empirical mass formula. It is obvious that it will be energetically favourable to fill up both shell systems rather than to have a large excess of protons or neutrons.

We also observe experimentally that larger nuclei tend to have an excess of neutrons. We can explain this by considering the Coulomb repulsion between protons. This means that the total potential is not identical for protons and neutron, i.e. they sit in slightly different potentials with slightly different energy levels. Since the Coulomb force opposes the nuclear force, the protons sit in a shallower well with slightly higher energy levels. Hence why we might expect neutrons levels to fill up slightly faster.

Why does this have more of an effect for heavier nuclei? Recall that the Coulomb force is proportional to \(Z(Z-1) \approx Z^2\) while the nuclear force is proportional to \(A\). So for larger nuclei the Coulomb force is relatively more significant, and so the difference in the energy levels between the proton and the neutron shells becomes greater.

Dipole and Quadrupole Moments

The nuclear magnetic dipole moment is given by: \[\mu = \mu_N(g_l L_z + g_sS_z),\]

where \(\mu_N\) is the nuclear magneton (a constant), \(g_l\) is the gyromagnetic ratio associated with orbital angular momentum, \(g_s\) is the gyromagnetic ratio associated with spin angular moment, \(L_z\) is the z-component of the orbital angular momentum, and \(S_z\) is the z component of the spin. (Note here that the capital ‘\(L\)’ and ‘\(S\)’ have been used to distinguish the physical quantities from quantum numbers.)

\(g_l\) is a convenient notation to express the fact that the orbital angular momentum of the proton contributes to the magnetic dipole moment, but that orbital angular momentum of the neutron does not (since it is uncharged). Hence \(g_l\) is 1 for protons and 0 for neutrons.

As discussed previously, the spin of both protons and neutrons does contribute, with \(g_s = 5.59\) for protons and \(g_s = -3.83\) for neutrons.

We can also predict electric quadrupole moments. If you are not familiar with quadrupole moments, essentially we can think of a progression from a single monopole, through an electric dipole (which you studied in PHYS5040), which has a separation of charges and hence an axis, to higher order shapes which have multiple poles. This is illustrated in Figure 3.

Certain nuclei are found to have large electric quadrupole moments, beyond anything which could be predicted by the shell model alone. This suggests that there is some non-spherical-uniformity to these nuclei and lends support to the idea of the Collective Model.

The Collective Model and Beyond

The shell model does not explain all the observed properties of nuclei. In particular, when we study nuclei in excited states, not all of the observed energy levels are predicted by the shell model. It turns out that there are three main ways that a nucleus can be put in an excited state

The first way is predicted by the shell model. The vibrational and rotational energy levels are not predicted by the shell model. Extending the shell model to include these effects leads to the Collective Model, so-called because the vibrational and rotational states involve the whole of the nucleus. We will not study these further, but you can read more about them in an appendix if you are interested.

In these first four lectures we have made a number of attempts to model the nucleus, ranging through the SEMF, our finite square well model of the deuteron, the simple shell model, the introduction of spin-orbit coupling and finally (briefly) the idea of the collective model. While all of these models have some success a at predicting experimental observations, it should be clear that none of them provides a complete description. They all attempt to simplify what is, in essence, an incredibly complex quantum-mechanical system of many interacting bodies. Of course there are many further complicated refinements to these models which are beyond the scope of this course, and research continues. Nevertheless, you will find the simple models we have developed useful we move on to study nuclear reactions and decays.