Physics and Astronomy, University of Kent
This section covers some of the fundamental properties of atomic nuclei. At this stage we will simply describe some simple properties and give definitions without any real attempt to explain why things are this way. In later sections we will try to develop models of the nucleus that allows us, to a greater or lesser extent, to predict some of these properties.
An atom consists of a positively charged nucleus surrounded by a cloud of negatively charged electrons. Atoms are typically \(10^{-10}\) m in diameter, a distance also known as an Angstrom, Å. You have studied atomic physics in detail previously and should review the basic properties if you do not remember them. In particular, the concept of electronic energy levels and quantum numbers will translate directly when we study the shell model of nuclei.
The nucleus contains protons and neutrons, which are collectively known as nucleons. A nucleus is typically \(10^{-14}\) m in diameter, four orders of magnitude smaller than the atom. We will therefore often work in lengths scales of femtometres (fm), \(10^{-15}\) m. Femtometres are also sometimes referred to as Fermis (after Enrico Fermi) which conveniently has the same abbreviation of fm. Nuclear diameters are usually in the range of 1 to 7 fm (we will come back to what exactly we mean by the diameter of a nucleus later). Since nucleons are not fundamental particles they have a finite diameter of around 1.7 fm. (The exact value is still under investigation1).
Nucleons are each made of three quarks. Protons have a charge of +1e, where \(e\) is the fundamental charge, \(1.6\times10^{-19}\) C. Neutrons are uncharged. The nucleus has a positive charge of \(Ze\) where \(Z\) is the number of protons. An atom with a full set of \(Z\) electrons of charge \(-e\) is therefore exactly neutral.
For energy we will work in units of electronvolts (eV). An electronvolt is the energy gained by an electron as it is accelerated through a potential difference of 1 V. 1 eV = \(1.6 \times 10^{-19}\) J. Energies dealt with in the nucleus are on the order of MeV (i.e. \(10^6\) eV) (often 10s of MeV). Compare this to atomic physics, where we are dealing with energies of merely 10s of eV. This is why nuclear reactions, which involve the nucleus, are a lot more powerful than chemical reactions, which involve electrons in atoms.
A nuclide is a specific combination of numbers of protons and neutrons. For any nuclide we write \(\rm ^A_ZX_N\) where
X is the chemical symbol for the corresponding element
Z is the atomic number
N is the number of neutrons
A = Z + N is the atomic mass number
However, since the chemical symbol allows \(Z\) to be looked up, and \(N = A -Z\), both \(Z\) and \(N\) are redundant information. So we will often instead see simpler notations such as \(^{56}\)Fe or Iron-56. Iron has an atomic number, \(Z\), of 26, and so this nucleus has \(N = 56 - 26 = 30\) neutrons.
It can still be sometimes useful to explicitly provide \(Z\) and \(N\) depending on the context, an example being when writing nuclear reactions where it makes it easier to check that everything is conserved.
We then have certain names for variations:
Isotopes: Nuclides with identical Z and different N
Isobars: Nuclides with identical A.
Isotones: Nuclides with identical N
Isomers: Long-lived excited states of nuclei.
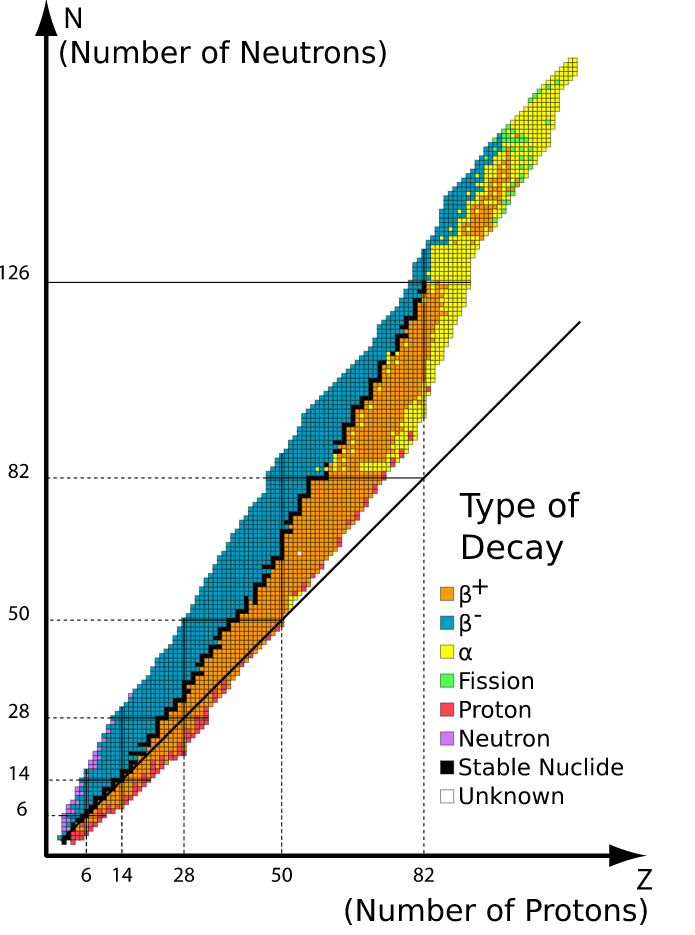
While there are only 118 different elements (different values of Z) there are over 3000 nuclides (with different values of N and/or Z) that have been experimentally observed, with around 330 occurring naturally. Of these around 250 are stable, in the sense that they do not decay over timescales comparable to the age of the universe. The nuclides found naturally correspond to only around 90 elements. That is to say that the list of stable nuclides includes isotopes of many elements (same number of protons but different number of neutrons). Stable nuclei typically have \(N\) slightly larger than \(Z\), i.e. slightly more neutrons that protons, as shown in Figure 1.

Most nuclides are spherical in shape, but some are deformed. We will discuss the reasons for this later on.
Nuclear masses are normally given in terms of the atomic mass unit, \(u = 1.661 \times 10^{-27}\) kg, which is 1/12th the mass of a neutral carbon atom. The mass of a proton is \(m_p = 1.00727u\), and a neutron is \(m_n = 1.0087u\). We also sometimes give masses in units of \(\mathrm{MeV/c^2}\), using the mass energy relationship \(E = mc^2\) (Consult your Stage 1 special relativity notes for more on this). We have then that \(1u = 931.5~\mathrm{MeV/c^2}\), so that nuclei have masses of a few \(\mathrm{GeV/c^2}\). Sometimes the \(\rm c^2\) is omitted for convenience and we refer to masses in units of \(\mathrm{MeV}\), you will see both forms during this module.
The masses of nuclei are slightly less than the sum of the masses of their constituent nucleons, typically by about 0.08\(u\) per nucleon (i.e. a nucleus with 100 nucleons would be about \(8u\) short.) This is known as the mass deficit or mass defect. The existence of the mass deficit is obvious for Carbon-12 which has a mass of exactly \(12u\); since protons and neutrons both haves masses of greater than \(u\), their total mass must be greater than \(12u\) even before we count the electrons. The mass deficit is associated with the binding energy of the nucleus which is discussed in the next section.
The mass of a nucleus can be measured with a mass spectrometer, where essentially a magnetic field bends a stream of ionised nuclei into an arc with a radius of curvature depending on the mass of the nuclei. Refer back to the PHYS3220 notes (provided on the PHYS6660 Moodle page) for details on the mass spectrometer, or see Krane Section 3.2. A mass spectrometer can also be used to find the relative abundance of different isotopes within a sample, since nuclides of each isotope will have a different mass and hence strike the detector of the mass spectrometer at a different point.
It was understood since the discovery of the electron in 1897 that atoms consist of positive and negatively charged elements. After he discovered the electron, J.J. Thompson proposed in 1904 the Plum Pudding Model, in which the negatively charged electrons are imagined to be distributed in some continuous positively charged medium. (If you’re wondering why this is a ‘plum pudding’, in those days people called raisins plums, so it is really a raisin pudding!) This model was not completely accepted and raised some questions over whether charges could penetrate each other.
In 1909, Hands Geiger and Ernest Marsden, under the supervision of Ernest Rutherford, were conducting experiments in Manchester. They were firing alpha particles at pieces of thin gold foil. You will study alpha emission later, but for now you should know that alpha particles are Helium nuclei, 2 protons and 2 neutrons, although at the time all was known was that they were small, positively charged pieces of matter. They expected that the alpha particles would be slightly deflected by the atoms making up the gold foil.
We can estimate the deflection we might expect using classical physics. If we have a uniform sphere of positive charge, with negatively charged electrons dotted within it, then near the surface of the sphere, unless we happen to be very close to an electron, the net charge is going to be positive. So the positively charged alpha particle will be deflected by a Coulomb force. Recall that the magnitude of the Coulomb force, \(F\), between two charges is \[F = \frac{k q_1 q_2}{r^2},\]
where \(k\) is Coulomb’s constant, \(q_1\) and \(q_2\) are the two charges and \(r\) is their separation. Referring to Figure 1, the change in the y component of momentum due to an impulse from the Coulomb force is given by
\[\delta p_y = F \delta t,\]
where \(\delta t\) is the interaction time, and a change in velocity of
\[\delta v_y = \frac{F \delta t}{m_\alpha},\]
where \(m_\alpha\) is the mass of the alpha particle.
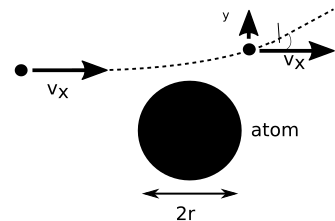
Let’s assume the force is significant while the alpha particle is close to the atom, as shown in the diagram, i.e. in a region of length \(2r\) where \(r\) is the radius of atom. If the alpha particle is initially travelling at a velocity of \(v_x\), then the interaction time will be \(2r/v_x\). So that:
\[\delta v_y = \frac{k q_1q_2}{m_\alpha r^2} \frac{2r}{v_x} = \frac{2k q_1 q_2}{m_\alpha rv_x^2}\].
Putting in the numbers give an angle \(\theta\) of less than \(0.02^o\). We have made a lot of assumptions and approximations here, but we can at least say that we expect a very small deflection.
What Geiger and Muller actually found was that some alpha particles were indeed deflected by a small angle while others seemed to pass through without any deflection at all. But some were scattered at huge angles, some even heading back the way they had come. These particles had clearly experienced a huge electrostatic force of repulsion. The only way that was possible would be if all of the positive charge was concentrated in a small area. If the alpha particle travelled through an area that was empty space, it would barely be deflected. But if it happened to go near or hit this dense region of positive charge, it would experience a large force of repulsion and be scattered at a large angle. This was the discovery of the nucleus, and the idea that the electrons orbited this positively charged centre.
Rutherford, Geiger and Muller refined this model over a series of further experiments, allowing them to estimate the size and charge of the nucleus. The model did have a huge problem (essentially that in classical physics, the electrons, as accelerating charges, would quickly radiate all their energy and spiral into the nucleus), which would later be solved by the quantum mechanical model of the atom.
Measuring the nuclear radius is not simple, particularly as there is no unambiguous boundary between being inside and outside the nucleus.
Let’s suppose we fire an alpha particle straight at a nucleus. It starts with some kinetic energy, \(E_K\). It will be slowed by Coulomb repulsion as it approaches the nucleus, eventually slowing to a complete stop before it begins to accelerate back away. The electrostatic potential energy a distance \(d\) from the nucleus will be \[U = \frac{1}{4 \pi \epsilon_0} \frac{(2e)(Ze)}{d},\]
where \(Z\) is the atomic number of the nucleus and \(e\) is the fundamental charge. At the turn-around point all of the kinetic energy has been transformed into electrostatic energy, so we have \(U = E_K\). From the known \(E_K\) we can therefore calculate the distance of closest approach, \(r\). In Rutherford’s experiment the alpha particles had kinetic energy of around \(E_K = 7.7\) MeV, giving \(r = 30\) fm.
However, this is only an upper limit on the radius. If we started with a more energetic alpha particle we would get a different value.
An alternative method is electron scattering. Recall the phenomenon of diffraction, whereby a wave is diffracted depending on the size of an aperture. If we fire high energy electrons at a nucleus, then the de Broglie wavelength of the electrons can be made comparable to the size of the nucleus. So when we detect the scattered electrons we observe diffraction rings. The radius of the first minimum is then related to the size of the nucleus.
For example, let’s suppose we fire some electrons with a de Broglie wavelength of \(3 \times 10^{-15}\) m at a nucleus. (The de Broglie wavelength is \(\lambda = h/p\), and for very fast electrons where the kinetic energy dominates over the rest energy, \(p \approx E_K/c\)). Let’s imagine we see a first order minimum at an angle of \(44^o\).
The angle \(\theta\) of the first minimum of the diffraction pattern from a circular apertures of diameter \(d\) is given by: \[\sin \theta = 1.22\frac{\lambda}{d}\]
Putting in the numbers for \(\theta = 44^o\) gives \(d= 4.3\) fm. Despite the approximations involved (e.g. treating a spherical object of unknown charge distribution as a uniform disc of charge) this turns out to be in agreement with other ways of estimating the size of a nucleus.
In general, the radii of nuclei are found to approximately follow the rule that: \[r = r_0A^{1/3}\] where \(r_0 = 1.25\) fm. (Slight variations on this value will be found in different texts). \(r_0\) does not have any particularly physical meaning; it is a fitted parameter. Note that since the volume of the nucleus is simply \(V \propto r^3\), this means that the volume is roughly proportional to the number of nucleons, \(A\), suggesting that the packing of the nucleons (and hence the nuclear density) doesn’t change much with \(A\).
We can now ask how exactly the charge of the nucleus is distributed within its volume. Experimentally this can be determined using more elaborate analysis of the scattering type experiments we have already discussed (see Krane Section 3.1 for details). It is found that the charge density is roughly constant up to a certain point, after which it decays down to zero, as shown in Figure 3. The distance over which the density drops from 90% to 10% of the value at the centre of the nucleus is called the skin thickness, or \(t\). Interestingly, this turns out to be largely independent of the atomic mass, with \(t \approx 2.3\) fm.
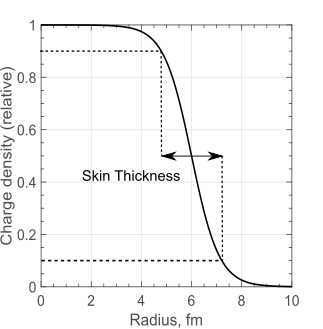
Note that, since electron scattering experiment involve only the Coulomb force, these are only telling us about the distribution of the charged nucleons, the protons. It could be, for example, that the neutrons are arranged entirely differently (for example surrounding the protons), giving a much large radius of nuclear matter (as opposed to radius of nuclear charge).
If we were to fire helium nuclei (alpha particles) at a heavier nucleus, as in Rutherford’s experiments, at sufficiently high energies we would begin to see effects due to the nuclear force which is felt by neutrons as well as protons (more on this in the next section). Detailed experiments (beyond the scope of this course) show that the radius of nuclear matter is very similar to the radius of nuclear charge, suggesting that the protons and neutrons are intermingled. We will therefore not really need to distinguish between these two definitions of the nuclear radius.
Most nuclides are unstable and decay over time periods ranging from fractions of a second to millions of years. The three most common types of decay (alpha, beta and gamma) are studied is more detail in Section 5, but briefly:
Alpha Decay is the emission of a helium nucleus (2p2n) and occurs mostly in heavier nuclei
Beta Decay is the emission of an electron or positron
Gamma Decay is the emission of a photon, and usually occurs alongside other kinds of decay
Regardless of the type of decay, the occurrence is stochastic - we cannot determine exactly when a decay will occur, only define the probability of it occurring within a certain time period. As each individual nucleus has its own independent probability of decaying, the decay rate of a sample depends on the number of non-decayed nuclei, \(N\) present, and so:
\[- \frac{dN}{dt} = \lambda N\]
where we have defined the constant of proportionality, \(\lambda\), known as the decay constant. The negative shows us that the number of non-decayed nuclei decreases with time.
The solution to this equation, obtained simply by separation of variables, is: \[N(t) = N_0 \exp{(-\lambda t)}\]
which shows us that the number of un-decayed nuclei drops exponentially.
We further define:
The activity, A as the number of decays in a sample per unit time. We define 1 (Becquerel) as 1 decay per second.
The half life, \(t_{1/1}\), as the time for half of the sample to decay
The specific activity, as the number of decays per unit time per amount of sample (e.g. measured by mass or number of nuclei).
When radiation interacts with matter, it deposits energy. We measure this dose in units of Grays, Gy, equivalent to 1 J/kg. When dealing with health effects of radiation, we instead use units of Sievert, Sv, which weights the dose to take account of the biological effects of the particular type of radiation. This is not discussed further here but if you are taking the medical physics module you will study this in detail.