Physics and Astronomy, University of Kent
Finally, we study the principles of nuclear fission and nuclear fusion, including some applications, and touch upon some modern developments.
Larger nuclei, particularly with \(A > 56\) (iron), can in principle release energy by fissioning (splitting) into two or more smaller nuclei with larger binding energy per nucleon, \(B/A\). We can distinguish between spontaneous and induced fission.
Consider U-238, an isotope of Uranium, with \(B/A = 7.6~\rm MeV\). If it were to split into two equal fragments, both with \(A = 119\), then the SEMF predicts that they would each have \(B/A = 8.5~\rm MeV\), yielding a huge total energy release of \((8.5 - 7.6) \times 238 = 214~\rm MeV\). And yet the half life for this decay to occur spontaneously is \(10^{16}\) years! The first question to answer is therefore, why don’t all heavy nuclei undergo fission until they reach Fe-56?
The simplest answer to this question is a similar one to what limits the rate of \(\alpha\)-decay - the Coulomb barrier. We can imagine the parent nucleus just at the point of splitting. Each fragment sits in a potential well, and must overcome the Coulomb barrier to escape. As with the \(\alpha\)-decay, we can estimate the height of the barrier by considering the point where the two fragments are just touching. Each has a radius of
\[\begin{equation} r = (1.2~\mathrm{fm})A^{1/3} = (1.2~\mathrm{fm})(119)^{1/3} \approx 6~\mathrm{fm} \end{equation}\]
and so the separation is \(r_s = 12~\mathrm{fm}\). The electric potential is then \[\begin{equation} V = k\frac{q_1q_2}{r_s} = 250~\mathrm{MeV} \end{equation}\] where \(k \approx 1.44 \rm\, MeV\,fm\).
In this case this is sufficiently far above the \(214~\mathrm{MeV}\) energy release (i.e. the excess energy that the fission products would have) that we might expect that the probability of tunnelling through the barrier is low, and indeed this is the case. However, in other cases this is not so clear cut, and we can find possible fissions that, by this calculation, should occur readily, but in fact do not.
Greater understanding can be obtained by using the liquid drop model to consider what happens as the nucleus splits. In order to divide into two fragments it must first deform and become elongated. Considering the SEMF, we would expect the volume term to not change (since it concerns neighbouring nucleons), the surface term to increase (since the surface area increases) and the Coulomb term to decrease (since the protons are, on average, more spaced out). The outcome therefore depends on how these two changes balance. If the Coulomb term decreases faster than the binding energy increases as the nucleus is stretched then the process will run away until it fissions. If the increase in the surface term dominates then the stretching reduces binding energy and so the nucleus will tend to hold together.
Mathematically, we can approximate the surface area of an ellipsoid by the first two terms of a Taylor series: \[\begin{equation} S = 4\pi R^2 (1 + \frac{2}{5}\epsilon^2) \end{equation}\] where \(\epsilon\) is the eccentricity of the ellipse and \(R\) is the radius of a sphere of the same volume. The increase in the average separation between points within the volume (which is relevant for the Coulomb term) goes as: \[\begin{equation} D = (1 - \frac{1}{5}\epsilon^2) \end{equation}\]
The change in binding energy for a given eccentricity relative to an unstretched nucleus is therefore: \[\begin{align} \Delta B &= B(\epsilon) - B(\epsilon = 0) \\ &= - a_s A^{2/3}(1 + \frac{2}{5} \epsilon^2) - a_cZ^2A^{-1/3}(1-\frac{1}{5}\epsilon^2) + a_sA^{2/3} + a_cZ^2A^{-1/3} \\ &= (-\frac{2}{5}a_sA^{2/3} + \frac{1}{5}a_cZ^2A^{-1/3})\epsilon^2 \end{align}\]
In practice, regardless of the value of \(\epsilon\), stretching increases the binding energy (i.e. releases energy) when \[\begin{equation} \frac{1}{5}a_cZ^2A^{-1/3} > \frac{2}{5}a_sA^{2/3} \end{equation}\]
Putting in the values for \(a_s\) and \(a_c\) this gives \[\begin{equation} \frac{Z^2}{A} > 47 \end{equation}\] as the condition for when fission should occur. In practice the condition can be slightly relaxed, as ever, due to quantum tunnelling, but this nevertheless gives us a rough estimate. Nevertheless, if we were to put in the values for U-235 (Z = 92, A = 235) we get \(Z^2/A = 36\), suggesting that spontaneous fission should not readily occur.
There are certain nuclei which do not undergo spontaneous fission but that can nevertheless be made unstable to fission by absorption of a neutron. The neutron may carry kinetic energy, or may be a thermal neutron, meaning that it carries only the energy associated with the temperature of the environment (\(E=k_BT\)). Some nuclei, such as U-235, will fission just from absorbing a thermal neutron. Such nuclei are said to be fissile. Others, such as U-238, require the neutron to carry kinetic energy. These are fissionable, but not fissile.
Following the absorption of the neutron, we obtain a compound state (excited state). The excitation energy of this state is obtained from the mass difference between the excited compound state and the equivalent ground state nucleus. For example, if U-235 absorbs a neutron, to form the compound state \(^{235}\mathrm{U}^*\), then the excitation energy is \[\begin{equation} E_{\mathrm{ex}} = m(^{236}\mathrm{U}^*) - m(^{236}\mathrm{U}), \end{equation}\] where \[\begin{equation} m(^{236}\mathrm{U}^*) = m(^{235}\mathrm{U}) + m_n, \end{equation}\] where \(m_n\) is the neutron mass. This gives \(E = 6.5~\mathrm{MeV}\), sufficient to overcome the activation energy (energy to overcome to fission barrier) of \(6.2~\mathrm{MeV}\).
In comparison, for U-238, the same calculation gives \(E_{ex} = 4.8~\mathrm{MeV}\) which is insufficient to overcome the activation energy of \(6.6~\mathrm{MeV}\). (The difference can be understood in terms of the pairing term of the SEMF, since U-235 is even-odd and U-238 is even-even). The extra energy for fission must therefore come from kinetic energy of the neutron, hence why thermal neutrons cannot induce fission in U-238.
A general induced fission reaction of U-235 looks like:
\[\begin{equation} \text{n} + {}^{235}_{92}\text{U} \rightarrow {}^{236}_{92}\text{U}^* \rightarrow \text{X}^* + \text{Y}^* \rightarrow \text{X} + \text{Y} + \kappa \text{n} \end{equation}\] where \(\text{X}\) and \(\text{Y}\) are the decay products and \(\kappa \approx 2.4\) is the average number of prompt neutrons which are released almost immediately (\(10^{-14}~\mathrm{s}\)).
While we might expect that \(\text{X}\) and \(\text{Y}\) would be roughly equal in size, this is not the most probable outcome. Typically the fission fragments from U-235 are around \(A = 95\) and \(A= 137\). The exact reasons for this are still being worked out, but are thought to be connected to shell filling effects.
Even after the emission of the prompt neutrons, this decay products still have an excess of neutrons and hence are unstable. \(\beta\)-decay often follows, followed by further emission of neutrons, known as delayed neutrons as they are emitted around 1 s after the fission. These only make up less than 1% of the total neutrons emitted, but turn out to be very useful for fission power generation, as discussed below.
When a nucleus, such as U-235, undergoes fission, it results in two unequal daughter nuclei and several neutrons. The neutrons are emitted because the daughter nuclei have an excess of neutrons (recall that light nuclei require a smaller excess of neutrons to be stable.). These neutrons can then be absorbed by other U-235 nuclei, which then fission and release more neutrons. If, on average, each fission results in less than one subsequent fission, then the situation is sub-critical and things quickly stop. If each fission results in another fission then the situation is critical and we have a stable reaction. If each fission results in more than one further fission then we are super-critical and we have a run-away reaction.
To generate power from nuclear fission we would like to have a stable, self-sustaining, nuclear reaction. We certainly do not want something that runs away. Most nuclear power is generated using U-235. Naturally occurring Uranium only contains about 0.7% U-235, with the remainder mostly U-238 which is not fissile. For most nuclear reactors the Uranium must be enriched to increase the U-235 fraction to about 4% using a centrifuge. The waste product from this process, which has a lower concentration of U-235 and a higher concentration of U-238, is called depleted uranium and has several applications, including in armour-piercing shells.
With U-235 it turns out that, by default, the reaction is sub-critical. Even though several neutrons are produced by a fission, on average less than one will be absorbed by another U-235 nucleus. This is because they are created with sufficient kinetic energy that they are not easily absorbed. We refer to the chance of the neutron being absorbed as the cross-section. The cross-section rapidly decreases as the kinetic energy increases.
To achieve a self sustaining nuclear reaction we need to slow the neutrons down, i.e. thermalise them. This is done with a medium called the moderator. In a nuclear reactor this will often be graphite. Neutrons entering this material lose kinetic energy and then are more likely to absorbed by a U-235 nucleus, increasing the rate of fission. Layers of the nuclear fuel (Uranium) and moderator were traditionally referred to as the pile.
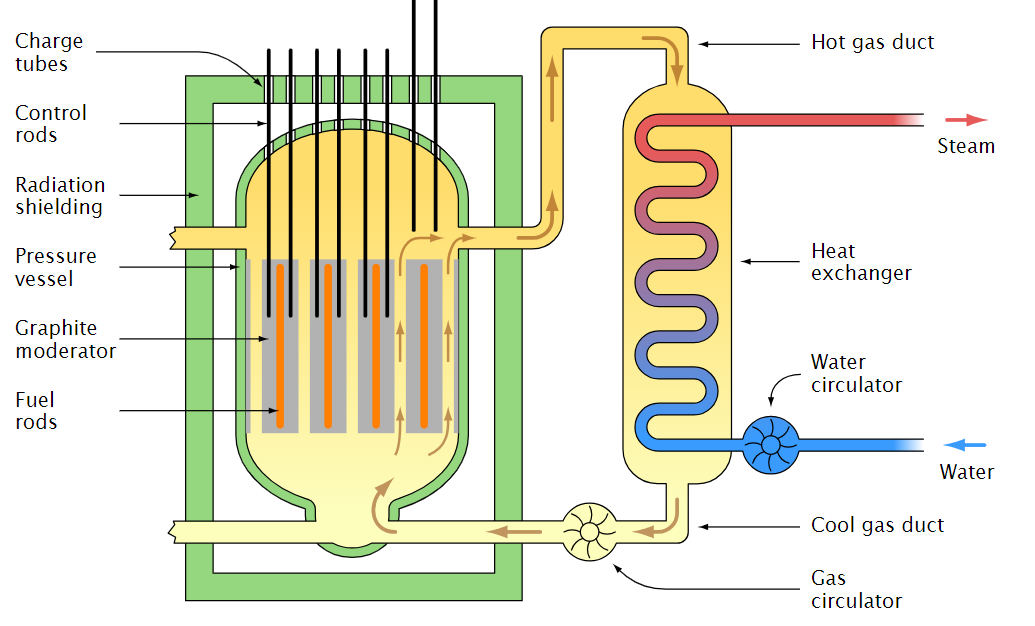
The rate of energy generation in a nuclear reactor is controlled by using the correct amount of moderator. The reaction rate can be fine tuned by inserting control rods of materials such as Cadmium or Boron which absorb neutrons and hence reduce the rate of the reaction. However, given the rate of the reaction and the emission of prompt neutrons, the control rods cannot be inserted or removed fast enough into a critical pile to prevent a run-away reaction and meltdown. This problem is solved by designing the pile to be slightly sub-critical for prompt neutrons. This means that the delayed neutrons are needed for the pile to become critical. Since these delayed neutrons are slower to be emitted, the control rods can be moved fast enough to tune the rate of fission and hence control the power generation. An example of a power station design is shown in Figure 1.

To generate power from a nuclear reactor we need to somehow capture the energy released by fission. Almost all of the energy goes into kinetic energy of the daughter particles, generating heat. Coolant, such as pressurised water or gas, flows through the reactor and transfers the heat to water which turns to steam and the expansion drives a turbine, just as in a conventional power station. As discussed above, the fission products are radioactive and must not be released directly into the environment. Some of the neutrons will also be absorbed by materials in and around the reactor, resulting in radioactive products. The whole of the reactor is therefore enclosed in a containment vessel.
This is all a gross simplification, and you don’t need to know any more details of how a reactor works for the exam, but for interest there are links to more detailed resources on Moodle.
To create a weapon we want to release as much energy as possible in a short space of time. We therefore want (a) lots of neutrons emitted (b) quickly. We therefore want increased purity of the fissile material (further enrichment), and make use of prompt neutrons. To generate a high yield, the key is to ensure that as much fission as possible occurs before the fissile material is blown apart. Approaches include gun-types, where two masses of the fissile materials are fired together, and implosion types, where a ring of explosives force the fissile material together in the centre. Links to more information are on Moodle.