Physics and Astronomy, University of Kent
In this section we will develop a simple quantum model of the simplest nucleus of interest - the deuteron. We begin with revision of some key ideas in quantum mechanics.
When you studied quantum and atomic physics, the simplest model for understanding atomic structure was the Hydrogen atom, consisting of a proton and an electron. While Hydrogen notionally has a nucleus, consisting of one proton, there is no nuclear force or potential involved, as we have only a single nucleon. So we will instead study a nucleus consisting of one proton and one neutron - called a deuteron (\(A = 2, Z=1, N = 1\)). (If we were to add an electron we would obtain an atom going by the perhaps more familiar name of deuterium).
We could also try to make nuclei with two nucleons (A=2) by putting together two protons or two neutrons. However, neither of these possibilities form stable nuclei; we will see why shortly.
While the (charge) radius of the deuteron nucleus is 2.2 fm, the average separation of the proton and neutron in a deuteron turns out to be 4.2 fm, larger than the expected range of the nuclear force. We therefore could predict that this is going to be a very loosely bound nucleus, and indeed we find a binding energy per nucleon of 1.1 MeV, much less than the typical 8 MeV for larger nuclei.
We will briefly review some quantum mechanics as a reminder of important concepts we will need later. This is not a detailed discussion; consult your notes from last year or textbooks for the details.
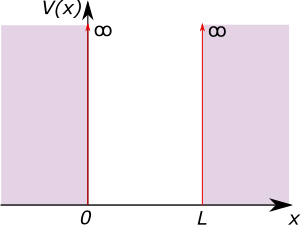
Consider a particle which sits in a 1D potential well (or ‘box’). Between position \(x = 0\) and \(x=L\) the potential, \(V\), is 0. Outside of this region, the potential is infinite. This is known as the infinite square well. \[V(x) = \begin{cases} 0, & \text{if}~ 0 < x < L \\ \infty,& \text{otherwise} \end{cases}\] and this is shown in Figure 1.

We can find the wavefunction for the particle, \(\psi\), using the time-independent, non-relativistic Schrödinger equation, \[-\frac{\hbar^2}{2m} \frac{d^2\psi}{dx^2} + V(x)\psi(x) = E\psi.\]
where \(\hbar\) is a constant, \(m\) is the mass of the particle, \(V(x)\) is the potential energy and \(E\) is the particle’s energy. If we solve this equation for the infinite potential well, we find that the wavefunction must be zero in the region of infinite potential, whereas inside the well it takes the general form \[\psi = A \sin kx + B \cos kx,\] where \[k = \frac{\sqrt{2mE}}{\hbar}.\]
However, the wavefunction must be continuous everywhere. Generally the derivative must also be continuous, but we will have to allow ourselves to sidestep this rule for infinite discontinuities in the potential (these aren’t terrible physical in any case, so we can think of this more of an abstraction rather than a real physical system). The first condition essentially means that the wavefunction must be zero at the box boundaries (\(x = 0\) and \(x=L\)), which means that only certain values of \(k\) are allowed, and also that \(B = 0\) (since \(\cos 0 \ne 0)\) If we substitute the wavefunction in and impose these conditions, we find the allowed energy values are: \[E_n = \frac{\hbar^2 \pi^2}{2mL^2}n^2 \quad \mathrm{where} \quad n \in \mathbb{N}\]
(Note \(\mathbb{N}\) is the set of natural numbers, or positive integers, 1,2,3 etc, so \(n \in \mathbb{N}\) means \(n=1,2,3...\)). The important thing here is that there are only discrete allowed energy levels for the particle, and that these are not evenly spaced.
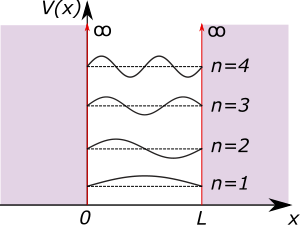
The corresponding wavefunction is \[\psi_n(x) = \sqrt{\frac{2}{L}}\sin(k_nx),\] where the normalisation factor is found by ensuring that \[\int \psi(x)^2 dx = 1.\] Given that the square of the wavefunction is the probability of finding the particle in the interval \(x + dx\), this is equivalent to saying that the probability of finding the particle somewhere in the box is 1. The first four wavefunctions are shown in Figure 2.
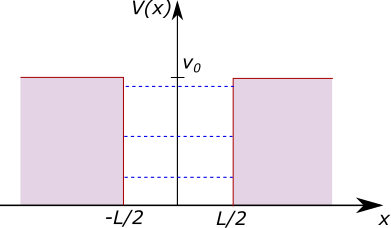
If we adjust our potential well so that the potential barrier enclosing the box is not infinite, giving a potential energy with some finite value \(V_0\), so that we have: \[V(x) = \begin{cases} 0, & \text{if}\ -L/2 < x < L/2 \\ V_0, & \text{otherwise} \end{cases}\] and if we assume that the particle has an energy \(E < V_0\), so that it is trapped in the box (classically), then the solution to the Schrödinger equation is different. We now have a non-zero wavefunction in the region with \(V(x) = V_0\), although this decays rapidly with distance from the edge of the barrier. After applying the wavefunction normalisability condition (i.e. ensuring that \(\psi\) does not go to infinity), we find solutions: \[\psi_2 = A\sin(kx) + B \cos(kx)\] inside the box (\(-L/2 < x < L/2\)), and solutions \[\psi_1 = C\exp(-\alpha x)\] and \[\psi_3 = C\exp(\alpha x)\] in the left (\(x < -L/2\)) and right (\(x > L/2\)) barrier regions, respectively.
Unfortunately there is no analytical solution this time, but some algebraic manipulation gets things into a form where solutions can be found numerically. It turns out that there are finite number of bound states (unlike the infinite square well which has an infinite number of solutions). Of course if \(E > V_0\) then the particle is no longer bound. The finite potential well and some example energy levels for a particular configuration are shown in Figure 3.
We can perform the same operation for other potentials. For example, the harmonic oscillator has a potential energy of the form \(V \propto x^2\) and has solutions with energy levels \(E_n = E(n + 1/2)\hbar \omega\) where where \(\omega\) is the angular frequency of oscillation (as defined classically). Here, again, there are infinitely many solutions, and in this case they happen to be equally spaced. Like the finite square well, positions outside of the well will have non-zero but decaying solutions.
To model the physical world we need to consider potentials in 3D. You have already seen this for the \(1/r\) Coulomb potential when you modelled the atom in PHYS5030.
Perhaps the simplest 3D potential is a cubical box of dimensions \(a \times a \times a\). The potential energy is: \[V(x,y,z) = \begin{cases} 0 & 0 \leq x \leq a, \quad 0 \leq y \leq a, \quad 0 \leq z \leq a \\ \infty & x < 0, \quad x >a, \quad y <0, \quad y> a, \quad z < 0, \quad z >a \end{cases}\] Outside of the box the potential is infinite and so \(\psi = 0\) here.
The 3D time-independent Schrödinger equation is \[-\frac{\hbar}{2m} \nabla^2 \psi + V\psi = E\psi,\]
or more explicitly in Cartesian co-ordinates \[-\frac{\hbar}{2m} \bigg (\frac{\partial ^2 \psi}{\partial x^2} + \frac{\partial ^2 \psi}{\partial y^2} + \frac{\partial ^2 \psi}{\partial z^2} \bigg) + V(x,y,z)\psi(x,y,z)= E \psi(x,y,z).\] Solving this for the 3D square box, we obtain eigenfunctions (wavefunctions) of the form \[\psi_{n_x, n_y, n_z} = \sqrt{\bigg (\frac{2}{a} \bigg)^2} \sin \frac{n_x \pi x}{a} \sin \frac{n_y \pi y}{a} \sin \frac{n_z \pi z}{a},\] with energy eigenvalues \[E_{n_x,n_y,n_z} = \frac{\hbar^2\pi^2}{2ma^2} (n_x^2 + n_y^2 + n_z^2).\] The solutions are now parameterised by three integers, \(n_x\), \(n_y\), and \(n_z\). The lowest possible energy state (the ground state) is (1,1,1). Notice that we have multiple states (i.e different wavefunctions with different corresponding probability density distributions) that have the same energy. For example, (1,1,2) and (1,2,1). These states are called degenerate.
It’s unlikely we will encounter cube-shaped potentials in nuclear physics. Instead we expect our potentials to be spherical, and it might be a reasonable first guess to assume that our potentials will be spherically symmetric, i.e. that the potential will only vary as function of distance \(r\) from the centre of the potential (a ‘central potential’). It is now natural to work in spherical polar co-ordinates (\(r\), \(\theta\), \(\phi\)) rather than Cartesian co-ordinates, for reasons that are hopefully obvious.
The Schrödinger equation in spherical co-ordinates looks unpleasant, \[-\frac{\hbar}{2m} \bigg[ \frac{1}{r^2} \frac{\partial}{\partial r} \bigg(r^2 \frac{\partial \psi}{\partial r} \bigg) + \frac{1}{r^2\sin\theta} \frac{\partial}{\partial \theta}\bigg( \sin \theta \frac{\partial \psi}{\partial \theta} \bigg) + \frac{1}{r^2 \sin^2\theta} \frac{\partial^2 \psi}{\partial \theta^2}\bigg] + V(r,\theta \phi)\psi(r, \theta, \psi) = E\psi(r, \theta, \psi)\]
but can now simplify things greatly by assuming a separable solution of the form: \[\psi(r, \theta, \phi) = R(r) \Theta(\theta) \Phi(\phi)\]
The important thing to realise is that as the potential is only a function of \(r\), and not \(\theta\) or \(\phi\), it is only the \(R(r)\) part of the solution that depends on the potential. The angular part, \(\Theta(\theta) \Phi(\phi)\), can be solved independently of the potential.
The solutions to the angular part are called spherical harmonics, which you have already studied in PHYS5030 (and saw some associated mathematics in PHYS5880). These solutions are parameterised by two quantum numbers: \(l\) and \(m_l\), the angular momentum quantum number and the magnetic quantum number. For a given \(l\) there are \(2l + 1\) possible values of \(m_l\), with \(m_l = 0, \pm 1, \pm 2, ... \pm l\). Solutions with different \(m_l\) but the same \(l\) have the same energy, such that states are \((2l + 1)\)-fold degenerate.
The radial part (known as the radial equation) can be re-written as \[-\frac{\hbar}{2m} \frac{1}{r^2} \frac{\mathrm{d}}{\mathrm{d}r} \bigg( r^2 \frac{\mathrm{d}R}{\mathrm{d}r}\bigg) + \bigg[ V(r)+ \frac{ \hbar^2l(l+1)}{2mr^2} \bigg ] R = ER.\] Check back in your PHYS5030 to see how this is obtained, but you should recognise that this now looks very similar to the 1D wave equation but with a modified ‘effective’ potential, \[V_{eff} = V(r)+ \frac{ \hbar^2l(l+1)}{2mr^2}\] We also have to be a bit careful because we now have that \(r>0\) which matters when we choose the boundary condition at \(r=0\). The \(l\) is the angular momentum quantum number, discussed more below.
The solution for radial part of the wavefunction, \(R(r)\), depends on the specific potential we are dealing with. Solutions to the radial part are parameterised by \(n\) and \(l\), but the exact form and the allowed values of \(l\) depend on the potential. For example, in atomic physics when you looked at the Hydrogen atom using the Coulomb (\(1/r)\) potential, you found that \(l = 0,1,2,3 ... (n-1)\) and that the energy does not depend on \(l\). In this case each energy level works out to be \(n^2\)-fold degenerate.
Finally, a quick reminder on the quantum theory of angular momentum (again, consult your PHYS5030 notes for the details). Angular momentum is a vector, \(\vec{L}\), but unlike in classical physics, it is not possible to know the three components of the angular momentum vector simultaneously (i.e. the operators for the x, y and z components do not commute). By convention we choose to specify two quantities: the magnitude of the angular momentum, \(L\) (or sometimes the magnitude squared \(L^2\)), which does commute with the three components, and the z-component, \(L_z\). The \(L_x\) and the \(L_y\) components are then unknown.
In the case of spherical harmonics, the magnitude of the angular momentum and the z-component of angular momentum are related to the quantum numbers \(l\) and \(m_l\). \[L = \hbar \sqrt{l(l+1)}\] \[L_z = \hbar m_l\]
There is another type of angular momentum which is intrinsic to particles, called spin. Unlike the angular momentum we have defined above, which for atoms and nucleons is generally referred to as ‘orbital angular momentum’ by analogy with a planetary-type model where electrons are orbiting the nucleus, the spin has less obvious classical analogies. Again, spin is a vector \(\vec{S}\), and we parameterise the spin in terms of quantum numbers \(s\) and \(m_s\), with the spin magnitude: \[S = \hbar \sqrt{s(s+1)}\] and the \(z\)-component: \[S_z = \hbar m_s\]
Unlike the orbital angular momentum, for which the \(l\) and \(m_l\) take integer values, fermions have a spin quantum number of \(1/2\), with \(m_s = \pm 1/2\).
The total angular momentum is the vector sum of the orbital and spin angular momenta: \[\vec{J}= \vec{L} + \vec{S}\]
Again we have quantum numbers \(j\) and \(m_j\) which parameterise the magnitude \[J = \hbar \sqrt{j(j+1)}\] and the \(z\)-component \[J_z = \hbar m_j\] where this time we have \(m_j = -j, -j +1, ... j-1, j\).
We call this effect the coupling of the orbital and spin angular momenta. A little bit of thought should allow you to check that: \[m_j = m_l + m_s = m_l \pm 1/2\] Given that \(m_l\) is an integer, we will always have that \(m_j\) is a half integer (-1/2, +1/2 etc), and hence \(j\) will also be a half integer. In fact we can see that \(j\) can either be \(l + 1/2\) or \(l-1/2\)
Modelling the deuteron is a two body problem: the interaction between two nucleons. As for any two-body problem we can treat this as a central force problem, i.e. we are considering one of the nucleons to be at the centre of the potential. We then work with the reduced mass. Here we have a proton and a neutron and the reduced mass is \[M = \frac{m_pm_n}{m_p + m_n}.\] However, since \(m_p \approx m_n\), and we are making a first order approximation here, we can use some nominal approximate mass \(m\) for both nucleons, such that \(M \approx m/2\).
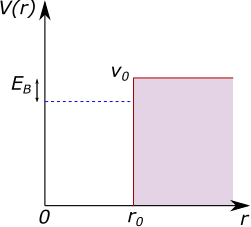
Unfortunately, we don’t know what the potential due to the nuclear force looks like. So let’s guess that it is a finite radial square well, as shown in Figure 4. This looks similar to the 1D potential well we reviewed above, but bear in mind this is a 3D system for which we are plotting against the radius and that \(r > 0\), which has some consequences for what must happen to the wavefunction at \(r=0\).
We now need to solve the Schrödinger equation in 3D: \[\bigg[ -\frac{\hbar}{2M} \nabla^2 + V(r) \bigg] \psi(r,\theta, \phi) = E \psi(r, \theta, \phi)\] where we have used \(\nabla^2\) to represent the Laplacian.
As discussed above, for a spherically symmetrical potential the solution is separable: \[\psi_{n,l,m} (r, \theta, \psi) = R_{nl}Y_{lm}(\theta, \phi)\] where we have indicated that we expect the solutions to be paramaterised by the three quantum numbers \(n\), \(l\), and \(m_l\).
The radial component of the wavefunction, \(R(r)\) satisfies the radial equation:
\[\bigg( - \frac{\hbar^2}{2m} \bigg( \frac{d}{dr^2} + \frac{2}{r}\frac{d}{dr} \bigg) + V(r) + \frac{\hbar^2 l (l+1)}{2mr^2} \bigg) R(r) = -E_bR(r)\]
(Check back in your PHYS5030 notes to see how this is determined).
Let’s begin by making the assumption that we are in the \(l=0\) solution which is spherically symmetric (i.e. the wavefunction has no dependence on \(\theta\) and \(\phi\)). So we only need to find the \(R\) part of the wavefunction. And setting \(l=0\) means that the radial part is also simplified to:
\[\bigg( - \frac{\hbar^2}{2m} \bigg( \frac{d}{dr^2} + \frac{2}{r}\frac{d}{dr} \bigg) + V(r) \bigg) R(r) = -E_bR(r) \label{eqn:R_comp}\]
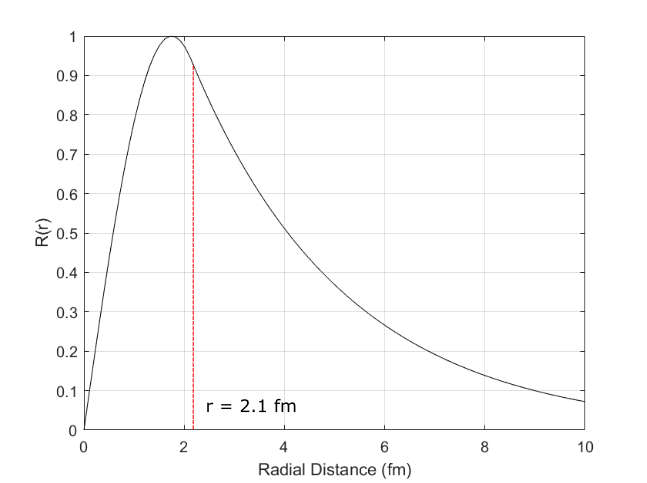
We don’t know the width of the square well, but let’s guess that it is the nuclear radius, \(r_0 = 2.1\) fm. So that we have: \[V(x) = \begin{cases} 0, & \text{if}\ 0 < r < r_0 \\ V_0, & \text{otherwise} \end{cases}\]
The depth of the nuclear potential energy well \(V_0\) is unknown. We do, however, know the binding energy, \(E_B = 2.225\) MeV, for a deuteron (measured via the mass defect or by the gamma ray energy released when a proton and neutron fuse). The depth of the well must be larger than this, otherwise the deuteron wouldn’t be bound.
To simplify things, we will rewrite this in terms of \(rR\) rather than \(r\). This will allow us to simplify things because
\[\frac{d^2}{dr^2}(rR) = \frac{d}{dr} \bigg( r\frac{dR}{dr} + R \bigg) = \frac{dR}{dr} + r\frac{d^2R}{dr^2} + \frac{dR}{dr} = r\frac{d^2R}{dr^2} + 2 \frac{dR}{dr}.\]
Using this result we can write Equation [eqn:R_comp] in a simpler form, and are now looking for a solution (wavefunction) that satisfies the differential equation:
\[\frac{d^2}{dr^2} rR - \frac{M}{\hbar^2}[V(r) + E_b](rR) = 0\]
Note that we have also used that the reduced mass \(M = m/2\).
The square well model means that the potential energy \(V(r)\) is a discontinuous step function. We can therefore find piecewise solutions, one for the region outside the well satisfying: \[\frac{d^2}{dr^2}(rR) - \frac{M}{\hbar^2}(V_0 - E_b)(rR) = 0\] and one for the region inside the well, satisfying:
\[\frac{d^2}{dr^2}(rR) - \frac{M}{\hbar^2}E_b(rR) = 0\] where we have used that \(V_0 = 0\) inside the well.
Taking inspiration from the 1D finite well, if we define wavenumbers \(k\) and \(K\) in the normal way, such that \[k = \frac{\sqrt{2ME_b}}{\hbar} ,\] and
\[K = \frac{\sqrt{2M(V_0 – E)}}{\hbar} ,\] then we can then write the differential equations in a simpler form: \[(rR)'' + K^2(rR) = 0\] and \[(rR)'' – k^2(rR) = 0\]
The solutions are \[rR(r) = \begin{cases} a \sin Kr & r < r_0 \\ b \exp(-kr) & r > r_0 \end{cases}\]
Note that mathematical solution \(\cos (Kr)\) inside the well would cause problems at \(r = 0\) and \(\exp(kr)\) outside the well would not be normalisable, so we have rejected these solutions as unphysical.
We now apply the boundary condition of the continuity of \(rR\) and \((rR)’\) at the discontinuity in \(V_0\). With a little bit of manipulation, we obtain: \[K \cot K r_0 = -k\]
Referring back to the definition of \(K\) and \(k\) we see that they are in terms of experimentally measurable quantities, \(M\) and \(E_B\), and the unknown potential \(V_0\). We can therefore solve (numerically) for potential, giving us \(V_0 \approx 35\) MeV. This is shown in a Jupyter notebook here: https://mybinder.org/v2/gh/MikeHughesKent/nuclear/master?filepath=deuteron.ipynb.
(Compare this to a standard quantum mechanical problem where we would be given \(V_0\) and would solve for the energy \(E_B\).)
From the plot of the deuteron wavefunction in Figure 5, we can see that it extends significantly outside of the well, meaning that the nucleons have a large probability of being separated by more than the interaction range of the nuclear force. (As we said earlier, the mean distance is 4.4 fm, despite the well radius of around 2 fm.)
In this model there is only a single bound solution – there are no bound excited states. Even in the ground state the nucleons are very close to the top of the well. This is also what is found experimentally, i.e. we do not observe excited states of the deuteron.
We assumed in the above that the deuteron is in an \(l=0\) state, but is that correct? To investigate this, we are now going to work out the angular momentum of the deuteron, which is a combination of the spins and orbital angular momenta of its constituent proton and neutron. Recall that the total angular momentum is the vector sum of the spin (intrinsic) angular momentum, \(\vec{S}\) and the orbital angular momentum (\(\vec{L}\)). Protons and neutrons are fermions, with spin 1/2. The total of their spin is the vector sum: \[\vec{S} = \vec{S_n} + \vec{S_p}\] Depending on whether the spins are parallel or anti-parallel, (i.e. whether the \(m_s\) have the same or opposite sign) this means that the total spin magnitude quantum number for the deuteron can be \(s=0\) or \(s=1\), depending on whether the two spins are aligned or anti-aligned.
Recall that there are \(2s + 1\) possible values for the z-component of spin, \(m_s\).
If the deuteron has \(s = 0\) (anti-parallel spins which sum to 0), there is therefore only one possibility, \(m_s = 0\). We call this a singlet.
If \(s=1\), we have three possible values, \(m_s = -1, 0, +1\). This is called a triplet.
Now we also need to take in account the orbital angular momentum to obtain the total angular momentum for the deuteron. (Slightly confusingly this is usually called the ‘spin’ of the nucleus, but remember that it includes the orbital angular momentum of the nucleons as well as their spins). \[\vec{J} = \vec{L} + \vec{S}\]
Note that this is a vector equation. First try to imagine this classically (Figure 6). If \(\vec{L}\) and \(\vec{S}\) are aligned, we would end up with a vector \(\vec{J}\) with a magnitude (length) of \(|L + S|\). If they were anti-aligned (i.e. pointing in opposite directions) we would have a vector of length \(|L-S|\). If there was some other angle between the vectors, we would end up with a some intermediate length \(|L-S| \leq J \leq |L+S|\).
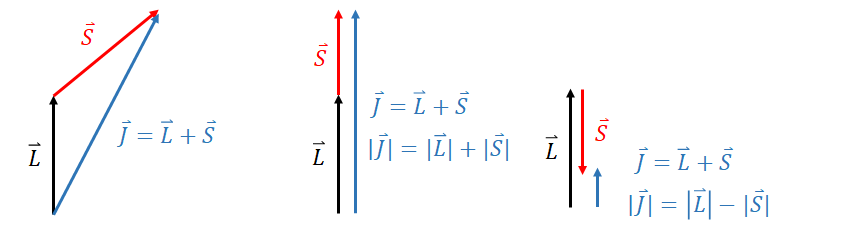
In quantum mechanics, \(J\) comes in discrete units, such that \(J = \hbar \sqrt{j(j + 1)}\) where the quantum number \(j\) is an integer. So the quantum number, \(j\), takes integer values such that \(|l-s| \leq j \leq |l+s|\).
While we assumed that \(l=0\) when we found the wavefunction we don’t actually know that this is the case, so let’s consider some possibilities (for \(l < 3\)):
If \(l = 0, s = 0\), then \(j = 0\)
If \(l = 0, s = 1\), then \(j = 1\)
If \(l = 1, s = 0\), then \(j = 1\)
If \(l = 1, s = 1\), then \(j\) could be \(0,1,2\)
If \(l = 2, s = 0\), then \(j = 2\)
If \(l = 2, s = 1\), then \(j\) could be \(1,2,3\)
Experimentally, we measure \(j=1\). This rules out those combinations where \(j\) cannot be 1. The possibilities we are left with are: \(^3S_1\), \(^1P_1\), \(^3P_1\) and \(^3D_1\). (Higher values of \(l>2\) also cannot have \(j=1\), which you can easily check).
Here we have introduced a new notation, related to the spectroscopic notation you saw in Atomic Physics. The letter (e.g. \(S, P\)) tells us the \(l\) quantum number (recall \(S\) is \(l = 0\), \(P\) is \(l = 1\), \(D\) is \(l = 2\), and \(F\) is \(l=3\)). The superscript is the number of \(m_s\) states (i.e. \(2s + 1\)), which tells us \(s\), and the subscript is the value of the quantum number \(j\). So in general, we write \(^{2s + 1}X_j\) where \(X = S,P,D,F...\).
(Note that when we refer to the total angular momentum of the nucleus, or the ‘spin’ of the nucleus, we often use the symbol \(I\) rather than \(j\). )
So which of these states is correct? To determine this we need some more experimental information. Luckily, we have just that.
We now need to introduce an important concept called parity, sometimes indicated by \(\pi\). Parity is a concept related to the symmetry of the wavefunction about the origin (the centre of the nucleus in our case). We call the case where \[\psi(-r) = \psi(r)\]
even parity, while: \[\psi(-r) = -\psi(r)\] is called odd parity. Even parity is often represented with a ‘+’, and odd parity is represented by a ‘-’.
While an arbitrary wavefunction will not have even or odd parity (formally it would not be an eigenfunction of the Parity operator), an important mathematical result is that states in a 3D potential (i.e. spherical harmonics) with an odd \(l\) have odd parity and states with an even \(l\) have even parity. Or, more neatly \[\text{parity} = (-1)^l\]
Experimentally, the deuteron is found to have even parity. This means that it must be in a state with an even \(l\). This rules out the \(p\) and \(d\) states, it must be in \(s\) or \(d\).
So we are nearly there, we have narrowed it down to two possible states, we just need a bit more information.
Whenever we have charged particles in motion we generate a magnetic field. We can see this using a classical analogy for atoms (imagine the charged electron circling the nucleus) but a similar effect occurs in the nucleus. This strength and orientation of this effect is called the nuclear magnetic moment.
The total magnetic moment is a combination of orbit and spin magnetic moments.
\[\mu = \mu_l + \mu_s\]
For the deuteron ground state we assumed initially that \(l = 0\), so there is no orbital angular momentum and hence no orbital magnetic moment. But we still have the spin - the intrinsic angular momentum - and so do expect a spin magnetic moment. We write this as: \[\mu_s = \frac{1}{2} g \mu_N\]
where \(\mu_N\) is the nuclear magneton (a constant which is a similar concept to the Bohr magneton studied in Atomic Physics), and is given by: \[\mu_N = \frac{e\hbar}{2m_p}\] (Recall from Atomic Physics that the definition of the Bohr magneton was the same, but with \(m_e\) replacing \(m_p\).
The factor of \(1/2\) is the spin and \(g\) is called the gyromagnetic ratio, it depends on the specific particle we are dealing with. Experimentally we find:
For a neutron, g = -3.8262.
For a proton, g = 5.586.
For an electron you may recall it is approximately -2.
Interestingly, this implies that the nucleus has a magnetic moment, despite it being uncharged. (The explanation for this is that, while the neutron has no net charge, it is made of quarks which are charged; it therefore has some internal distribution of charge).
So we can therefore calculate the magnetic moment of the deuteron, in terms of the nuclear magneton (which is a constant), by taking the (known) magnetic moments of the proton and the neutron and summing: \[\mu_d = \mu_p + \mu_n = (2.7928 - 1.9130)\mu_N = 0.8798 \mu_N\]
However, when the magnetic moment is measured, we find it to be \(0.85741 \mu_N\). How can this be?
We have accounted for the contribution of spin, but what about orbital angular momentum? We assumed that \(l=0\) and hence \(L = 0\), i.e. there was no orbital angular momentum.
This suggests that perhaps the deuteron is not in the \(^3S_1\) (\(l = 0\)) state after all. If it were in state with \(l \ne 0\) we would have some orbital angular momentum, and perhaps this would give us the experimentally observed magnetic moment.
We could try calculating the expected magnetic moment for \(^3D_1\) (we know we are not in \(l = 1\) because of the measured parity). Now we have \(l = 2\), so we also have a contribution from the orbital angular magnetic moment. Unfortunately when this calculation is done it turns out to give a total magnetic moment of \(0.310 \mu_N\), which is even worse.
The solution is that the nucleus exists in a superposition of these states. (In quantum mechanics we can make a new solution or state by weighted sums of solutions). That is, the total wavefunction would be: \[\psi = a_0 \psi_{l=0} + a_2 \psi_{l=2}\]
where \(a_0\) and \(a_2\) are constants such that \(a_0^2 + a_2^2 = 1.\) Then, from the normal rule of probabilities we have that \[\mu_d = a_0^2\mu_{l=0} + a_2^2\mu_{l=2}\]
Using the experimental value for the magnetic momentum of the deuteron, \(\mu_d\), then allows us to determine that \(a_0^2 = 0.96\) and \(a_2^2 = 0.04\). So the nucleus spends 4% of its time in an \(l=2\) state.
This suggests that our description of the nuclear potential wasn’t quite correct. It turns out that we weren’t quite okay to assume the wavefunction (and hence the potential) is spherically symmetric. We also know this from experiments, as the deuteron is found to have a quadrapole moment (more on this later). But it still gave us a good first approximation.
We can ask whether we would expect to see nuclei (i.e. bound states) with 2 protons (pp) or 2 neutrons (nn). Since we don’t observe these in nature, we need to be able to answer ‘no’!
It might be tempting to explain the non-existence of the pp nucleus by invoking the Coulomb repulsion; perhaps this is sufficient to modify the potential so that there is no bound state? However, this turns out not to be the answer, and in any case wouldn’t help us with the nn nucleus.
We observe experimentally that the dueteron has total spin of \(j = 1\), which for the \(l=0\) state must mean that the spins of the proton and neutron are aligned (giving us s = 1, the triplet state). We don’t find the deuteron in the s = 0 singlet state, where the spins are opposite. This suggests that the triplet state is energetically favourable. It turns out the the nuclear force is stronger between nucleons with their spins aligned, and in fact for a proton and a neutron with anti-aligned spins, there are no bound states.
So, in order to obtain a bound pp or nn state, we would need to have both protons or neutrons in the same spin state. But this is forbidden by Pauli’s exclusion principle. One would have to be in a higher energy state, and as already established this would turn out to be an unbound state, the energy would be too high. So we do not have pp or nn nuclei.
This also gives us some hints abut what is coming when we start to consider nuclei with more than 2 nucleons, and what the origin of the symmetry term in the SEMF might be.