Physics and Astronomy, University of Kent
In this section we begin to discuss how the nucleus is held together, introducing the concept of the nuclear force and binding energy. We will then develop a semi-classical model to predict the binding energy of different nuclei.
The Coulomb force cannot be the dominant force inside the nucleus, otherwise the positively charged protons would fly apart. We can therefore assume the existence of some force (which we will call the strong nuclear force) which overcomes the Coulomb repulsion within the nucleus. However, this force must be weak enough at the atomic scale not to interfere with the electron orbits, since we can model these perfectly well using only the Coulomb potential.
We therefore conclude that the nuclear force has a very short range. The maximum force is experienced by nucleons separated by around 0.8 fm and beyond 2 fm it increasingly becomes negligible. At distances shorter than 0.7 fm it becomes repulsive (stopping the nucleons penetrating each other). The force seems to apply equally well to protons and neutrons (otherwise there would be nothing keeping neutrons bound in the nucleus). In fact, experimentally it appears that the strong nuclear force attracts protons and neutrons equally to a very high level of precision.
Nucleons bound together in a nucleus are sitting in a potential well. To pull nucleons out of the nucleus we need to put in energy. Or, to put it another way, a nucleus is a bound (lower energy) state for this set of nucleons. The total energy required to completely separate all the nucleons is the binding energy of the nucleus. Alternatively, the binding energy is the energy that would be liberated were we to assemble a nucleus from its constituent nuclei.
If we were to introduce energy in order to break the nucleus apart, that energy would go into mass. Recall from relativity the relation \(E = mc^2\). The mass of a nucleus, \(M(Z, A)\), is less than the mass of its constituent protons, \(Zm_p = Z \times 1.00727u\), and neutrons \(Nm_n = N \times 1.0087u\). The difference is the binding energy, \(B(Z, A)/c^2\):
\[M(Z, A) = Zm_p + Nm_n - B(Z, A)/c^2\]
or
\[B(Z, A) = c^2[Zm_p + Nm_n - M(Z, A)]\]
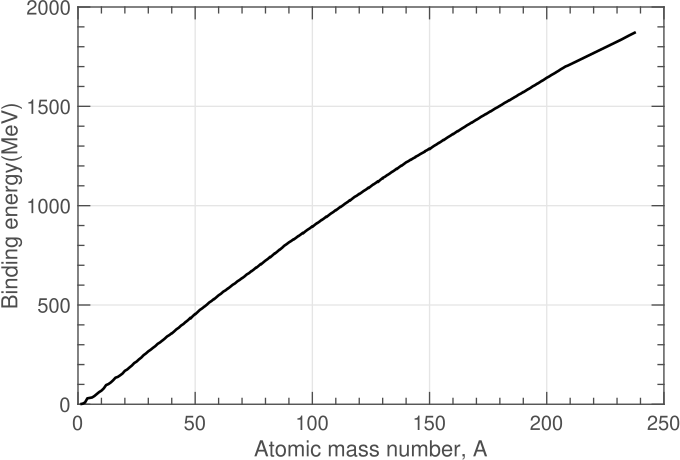
The binding energy is plotted for several hundred stable nuclei as a function of their atomic mass number, \(A\), in Figure 1. We can see that it increases with the number of nucleons (\(A\)) is a fairly, but not exactly, linear way.

A slightly more interesting plot is the binding energy per nucleon, \(B/A\) (i.e. the binding energy divided by the mass number), plotted for stable nuclei in Figure 2. The features now become clearer. For heavier nuclei, the binding energy per nucleon is just over 8 MeV, decreasingly slightly for heavier nuclei. For very light nuclei, the behaviour is a little more erratic, generally increasing with A, but with several outliers.
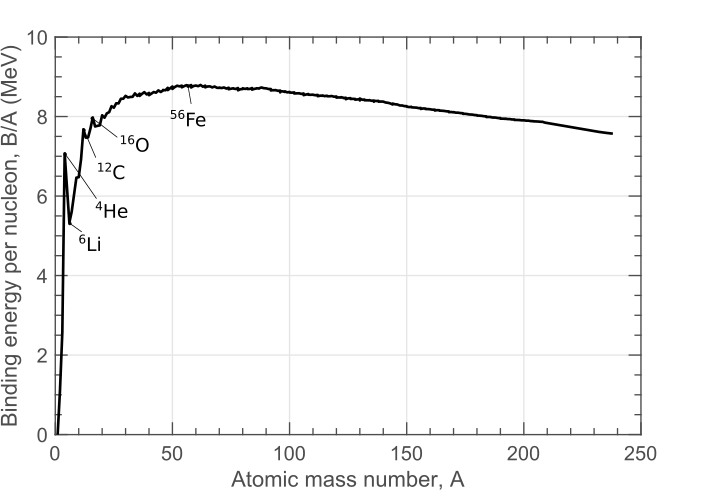
The peak of the curve is for \(\rm ^{62}Ni\), an isotope of nickel. However, sometimes \(\rm ^{56}Fe\) - iron - is highlighted as being the peak; while the \(B/A\) value is actually slightly lower, iron-56 is much more abundant in the universe than nickel-62 (due to lack of favourable pathways to produce nickel-62 in stellar nuclear synthesis). Iron-56 also has a smaller mass per nucleon because less of its mass is made of neutrons which are slightly heavier than protons.
This B/A peak marks a boundary between two effects - nuclear fission and fusion. You will learn more about these later, but essentially fission is the liberating of energy as two smaller nuclei join to form a larger nuclei, and fission is liberation of energy as a large nuclei breaks into smaller nuclei. We can see that fusion will only occur for an end product which is to the left of Nickel/Iron, since combining nuclei leads to a nucleus with a larger binding energy per nucleon. Since the number of nucleons remains the same, the total binding energy is now larger, meaning a release of energy. Fission will only occur to the right of Nickel/Iron if a nucleus splits into two smaller nuclei, they will have larger binding energy per nucleon, and so again, energy will be released.
For any nuclear reaction we can define the Q-Value. This is the difference between the sum of the binding energy of the nuclei before (\(M_i\)) and after (\(M_f\)) the nuclear reaction, or equivalently the change in the mass deficit before and after the reaction. It is given by
\[Q = (\sum M_i - \sum M_f )c^2\]
For example, consider the reaction fusing helium and carbon nuclei to form an oxygen nucleus:
\[^4_2He + ^{12}_6 C \rightarrow ^{16}_8O\]
Without worrying about the details of this type of nuclear reaction (which will be covered later), we can calculate the Q value by looking up the masses of these nuclei:
\[\begin{aligned} Q &= (4.00260u+12u - 15.99491u)c^2 \\ &= (0.00769u)c^2 \\ &= (0.00769)(931.5~\mathrm{MeV/c^2})c^2 \\ &= 7.16~\mathrm{MeV} \end{aligned}\] where we have used that \(u = 931.5~\mathrm{MeV/c^2}\).
This Q-value is positive: the mass of the products of the reaction are less than the mass of the reactants; the product is more tightly bound than the reactants; the binding energy is larger. We therefore have a release of energy. A reaction with a negative Q-value captures kinetic energy into binding energy. You will use the Q-value when you study nuclear reactions later in the course, and we will not delve into it more now. Trying to explain the shape of the B/A curve will be our next task.
In the above discussion we were only really talking about the magnitude of the binding energy. So is it positive or negative? With energy, signs and the zero crossing are a matter of convention, but we can think about the binding energy as being negative. The mass of a nucleus is less than the mass of its constituents, so we need a negative energy to give us that negative mass. This is consistent with the convention that we set the potential energy to zero when two particles are separated by an infinite distance. As they come together they then lose potential energy, and so the energy becomes negative. However, when talking about binding energy we often talk about it as a positive thing, such that nuclei with larger binding energy are more tightly bound, and we will adopt this convention in what follows.
The liquid drop model is based on the idea that a nucleus behaves in some respects like a drop of liquid – thought of as collection of bound molecules which are in constant motion. From this we can develop the semi-empirical mass formula, predicting properties of nuclei including binding energies, mass, stability and decays. The formula for the total binding energy is made up of a number of terms, each of which has a physically explainable (or at least plausible) origin, weighted by constants. Some of these weighting factors can be estimated from theoretical considerations, but in general they can only be determined accurately from fitting to experimental data. Hence why we talk about this as a ‘semi-empirical’ model.
As we saw previously, the binding energy per nucleon is approximately constant for all but the lightest nuclei, typically 8 MeV per nucleon. We therefore assume that each nucleon attracts its neighbours only, so that the total binding energy is proportional to the number of nucleons,
\[B_1 = a_v A,\]
where \(a_v\) is a constant to be determined. (If each nucleon attracted every other nucleon then this term would be roughly proportional to \(A^2\) which is definitely not what we observe.)
A nucleon on the surface of the nucleus has fewer neighbours than those near the middle. Therefore, nuclei with a larger surface to volume ratio will have a smaller binding energy. The volume is proportional to nucleon number, \(A\), and \(A \propto R^3\), where \(R\) is the nuclear radius. The surface area, \(S \propto R^2\) and so \(S \propto A^{2/3}\). The surface term is therefore
\[B_2 = -a_s A^{2/3},\]
where \(a_s\) is a constant to be determined. Note that it is negative since a larger surface area means a reduced binding energy.
Protons repel each other due to the Coulomb force. If we have \(Z\) protons then the number of interactions is \(Z(Z-1)\) (i.e. each proton repels each other proton). Recall the Coulomb force is long range, all the protons interact, so this varies roughly as \(Z^2\), unlike the volume term which varies as \(A\) rather than \(A^2\). The strength of the Coulomb force varies with inverse of separation (squared), and acts between all pairs of protons, so we expect a \(Z(Z-1)\) dependence. From electrostatics it is possible to show that the electrostatic energy of a sphere of radius \(r\) of uniform charge is:
\[U = -\frac{3}{5}\frac{Q^2}{4\pi\epsilon_0 r},\] where \(Q\) is the total charge and \(\epsilon_0\) is the permittivity of free space. Using \(Q = Ze\) and recalling \(r = r_0A^{1/3}\) gives us immediately
\[U = -\frac{3}{5}\frac{Z^2e^2}{4\pi\epsilon_0 r_0 A^{1/3}}.\]
However, this seems a little incorrect, since it would still give us some repulsion when \(Z = 1\), but a proton does not repel itself. So let’s write (without too much justification):
\[B_3 =- \frac{3}{5}\frac{Z(Z-1)e^2}{4\pi\epsilon_0 r_0 A^{1/3}} = -a_c \frac{Z(Z-1)}{A^{1/3}},\]
where \(a_c\) can be evaluated by substituting in the constants to be 0.72 MeV. Note that \(B_3\) is a negative term since the Coulomb force is repulsive.
If we were to use only the surface, volume and Coulomb terms then we would expect a nucleus made up entirely of neutrons to be more stable than one made up of protons and neutrons, since there is no Coulomb force to push them apart. This is obviously not what we observe. The next term in the equation, the symmetry term, tries to deal with this by invoking quantum mechanical arguments. From here on in, the terms are sometimes referred to as a ‘Fermi gas’ model rather than a liquid drop model.
Neutrons and protons are both fermions, and spin 1/2 particles. Pauli’s exclusion principle forbids identical fermions from occupying the same quantum mechanical state. This influences the nucleons’ states in the potential well, as only two nucleons (with opposite spin, more on that later) can occupy each state. But protons and neutrons are different particles, and so they have their own sets of states. Essentially, if we were to fill up a nucleus with just protons, they would fill up the higher energy states more quickly for a given \(A\) than if we had roughly equal numbers of protons and neutrons, each filling half as high in their own sets of states. (We will discuss this more when we talk about the shell model, for now we should just accept this.)
In general, this means than stable nuclei have approximately \(Z = A/2\), or roughly equal numbers of protons and neutrons. This is a very strong factor in the binding energy for small nuclei, slightly less so for larger nuclei which tend to be stable with a slight excess of neutrons (due to the closer spacing of higher energy levels, again we will discuss this more later). We can capture this \(A\) dependence with the following term:
\[B_4 = -a_{symm}\frac{(A-2Z)^2}{A} .\]
Since \(A = Z + N\) we can also write \[B_4 = -a_{symm}\frac{(N-Z)^2}{A}.\]
The physical justification for this form of the \(A\) dependence may not be so clear, but a bit of thought (or plotting it out) should convince you that this gives a term which increases the binding energy for \(Z\approx A/2\) more for lower \(Z\) nuclei than for higher \(Z\) nuclei.
Empirically it is found that nuclei with pairs of nucleons of the same type (e.g. 2p or 2n) have a higher binding energy than nuclei with one of each (1p + 1n). In fact, there are only 4 stable nuclei with an odd \(N\) and an odd \(Z\), and they are all fairly small (\(^2\)He, \(^6\)Li, \(^{10}\)B and \(^{14}\)N) compared to over 160 nuclei with even \(N\) and even \(Z\)! This is not accounted for by the terms we have introduce so far, so we need to add an additional term called the pairing term, sometimes labelled \(\delta\).
For odd \(A\) (either even \(Z\), odd \(N\) or odd \(Z\), even \(N\)), there is no effect, \(\delta = 0\)
For even \(A\) due to even \(Z\) and even \(N\), \(\delta = a_pA^{-1/2}.\)
For even \(A\) due to odd \(Z\) and odd \(N\), \(\delta = -a_pA^{-1/2}\).
Here \(a_p\) is our final constant to be determined. If you look in older books you may well find this term written as \(A^{-3/4}\) instead (In fact the justification for this power not being 1 is not obvious, why does the pairing term become less significant for larger nuclei?)
The total binding energy is the sum of the five terms (volume, surface, Coulomb, symmetry and pairing):
\[B(Z,A) = a_vA - a_sA^{2/3} -a_cZ(Z-1)A^{-1/3} - a_{sym} \frac{(A-2Z)^2}{A} + \delta\]
The constants are worked out empirically by fitting to measured binding energies of nucleons. A good set of values is:
\(a_v\) = 15.8 MeV
\(a_s\) = 18.3 MeV
\(a_c\) = 0.714 MeV
\(a_{sym}\) = 23.2 MeV
\(a_p\) = 12 MeV
Python code to fit values to experimental data is here: https://mybinder.org/v2/gh/MikeHughesKent/nuclear/master?filepath=SEMF.ipynb
The first three terms can be understood well in terms of a classical model of a nucleus. They are often referred to as the liquid drop model by analogy to a drop of liquid which is held together by molecular forces. The symmetry and pairing terms are quantum mechanical in nature, and are sometimes referred to as the Fermi gas terms; their origin and will be considered later in the context of the shell model.
To obtain the mass of a given nuclei, we now add up the masses of the constituent protons and neutrons and subtract the binding energy (because we made it a positive thing) divided by \(c^2\) (from \(m = E/c^2\)):
\[M(Z,A) = Zm_p + Nm_n - B(Z,A) / c^2,\]
or,
\[M(Z,A) = Zm_p + Nm_n - a_vA + a_sA^{2/3} + a_cZ(Z-1)A^{-1/3} + a_{sym} \frac{(A-2Z)}{A} - \delta.\]
Stable nuclei have high binding energies and hence low masses. Suppose we would like to find the most stable nuclide among all those with the same atomic mass number, \(A\). For a given number of nucleons, \(A\), we therefore want a minimum in the mass (largest binding energy), i.e.: \[\bigg( \frac{ \partial M}{\partial Z} \bigg ) _A = 0\]
Differentiating the expression for mass w.r.t \(Z\) gives
\[z_{min} = \frac{(m_n - m_p)c^2 + a_cA^{-1/3} + 4 a_{sym}}{2a_cA^{-1/3} + 8a_{sym}A^{-1}}.\]
Since \(a_c \ll a_{sym}\) the first two terms on the numerator are very small, and so \[z_{min} \approx \frac{A}{2} \frac{1} {1 + \frac{1}{4}A^{2/3} a_c / a_{sym}}.\]
When \(A\) is small \(\frac{1}{4}A^{2/3} a_c / a_{sym} \approx 0\) and so \(Z \approx A/2\). When \(Z\) is larger, \(Z/A \approx 0.4\). This is what we observe for stable nuclei in practice, and so the model is a good fit. Less stable nuclei decay into more stable nuclei (i.e. heavier nuclei decay into lighter nuclei (with the same \(A\)). This can be achieved by converting a neutron into a proton or a proton into a neutron (\(\beta\) decay - more on this later). Heavy nucleons that are far from the line of stability with excess neutrons may also decay by alpha emission (2 protons and 2 neutrons)