The notes below are a summary of the key points needed for the exam. For more details and background they should be read in conjunction with linked documents, papers or websites and the general reading:
Mertz, Introduction to Microscopy, Chapter 11.
Kim, Myung K. "Principles and techniques of digital holographic microscopy." SPIE reviews 1, no. 1 (2010): 018005.
If you are unfamiliar with scalar diffraction theory and the concept of the free space propagator, Chapter 2 of Mertz and Goodman’s ‘Introduction to Fourier Optics’ may also be useful background, although it is not essential.
Light is a wave in electric and magnetic fields, and so can be described by classical electromagnetic field theory (i.e. Maxwell’s Equations). Electric and magnetic fields are vector quantities, and a full treatment of light in this framework is quite complicated. Happily, it is often possible to make what is known as the ‘scalar wave approximation’, it which we describe light simply by the amplitude and phase of the electric field. Therefore, at any point in a light field, we can write \[E(x,y,z) = |E|cos\phi\] Here, \(E(x,y,z)\) is the electric field at each point in space (we will drop the explicit spatial dependence from now on, except when we need to clarify what we are talking about), \(|E|\) is the amplitude of the electric field at that point and \(\phi\) is the phase at that point. We can think of light as simply a 1D wave in the electric field, where \(E\) is the height (amplitude) of the wave, and \(\phi\) is the point along the wave (the phase).
Unless you are very good at manipulating trigonometric identities, it is often more useful to write this in a different way. Recall Euler’s formula:
\[e^{i\phi} = \cos \phi + i \sin \phi\]
where \(i=\sqrt{-1}\). So we can write:
\[E = \operatorname{Re}\{|E|{e^{i \phi}}\}\]
where \(\operatorname{Re}\{x\}\) denotes the real part of \(x\). This is known as the phasor representation (the \(e^{i \phi}\) part is the phasor). We sometimes refer to this as the complex field (because there is an \(i\) in there), although this is arguably slightly misleading as the field isn’t a complex number, because we take only the real part. In practice we don’t usually bother writing \(\operatorname{Re}\); we just remember that we take the real part at the end.
Recall that if we write a complex number in the following way:
\[C = a + ib\]
then the argument/phase \(\phi\) is given by \(\arctan(b/a)\) and the amplitude is \(\sqrt{a^2 + b^2}\).
Any kind of detector (cameras, photodetectors, photographic film, the human eye) is sensitive to the absolute square of the field, i.e.
\[I =EE^*=|E|^2e^{i\phi}e^{-i\phi}=|E|^2\]
where we have used that when we square a complex number, this means we multiply it by its complex conjugate.
This means that we don’t normally detect the phase part of the field, only the square of the amplitude.
If we know the field, \(E(x,y,0)\), at some initial plane, we can calculate the field at a distance \(z\) from this plane, \(E(x,y,z)\) using the diffraction integral from scalar diffraction theory. This is beyond the scope of the lecture, consult Goodman’s ‘Introduction to Fourier Optics’ for details.
However, a good approximation, known as the Fresnel approximation, can be used when the distance to the plane is comparable to the lateral extent of the field. In which case, we can calculate the field at a distance \(z\) by a convolution:
\[E(x,y,z) = E(x,y,0) \ast h(x,y,z)\]
where \(h(x,y,z)\) is the Fresnel propagator, given by:
\[h(x,y,z) = \frac{e^{ikz}}{i\lambda z}e^{i\frac{k}{2z}(x^2 +y^2)}\]
where \(\lambda\) is wavelength. We can think of this as being a bit like the PSF we defined in Lecture 1, although now we are in talking about what happens in free-space, rather than because of a lens, and it is acting on the complex field rather than the intensity.
In a transmission microscope, we obtain image contrast because parts of the sample absorb different amount of light. This means they reduce the \(|E|\) part of the field. However, as discussed in Lecture 1, many objects (such as cells) are not very absorbing, and so contrast can be quite low.
As light travels a distance \(z\) through a material of refractive index \(n\) (i.e. of optical thickness \(nz\)), the phase progresses by \(knz\) where \(k\) is the wavenumber. \[k= \frac{2\pi}{\lambda}\] and where \(\lambda\) is the wavelength. So, if we initially have some light with phase \(\phi\), then after passing through the material it will have a phase of: \[\phi'= \phi+nzk\] and so, \[E'= |E|e^{i[\phi + nzk]}\] Remember than our phase wraps round every time we get to \(2\pi\), since \(\cos \phi = \cos (\phi + 2\pi)\).
Now, if we consider a sample such as a cell on a microscope slide, the refractive index of the cell is different to the surrounding medium. So the light which has travelled through the cell will have a different phase to the light which hasn’t. So, if we could see the phase this would provide some extra contrast in the image. If we could measure the phase, we might also be able to measure the optical thickness of the cell (although this is complicated if the phase difference has gone past \(2 \pi\) and wrapped around). If we know the physical thickness this can tell us \(n\), or if we know \(n\) then it tells us the thickness.
A second benefit of phase imaging is that, once we have determined the complex field, we can use the Fresnel propagator to determine the field at other axial positions. This means we can numerically ‘focus’ at different depths in the sample without moving anything (or even go back and refocus our images later on). It also means that, in some cases, we can dispense with a lens altogether, and perform all the focusing numerically.
Phase contrast imaging is a very old idea, it was first developed in the 1930s and won Fritz Zernike the 1953 Nobel Prize in Physics. The idea is to somehow convert phase information into intensity information so that we can see it (either by eye or on a camera). This is possible using interference, because the intensity pattern produced by the interference between different beams depends on their relative phase.
There are two common methods: Zernike phase contrast and Differential Interference Contrast (DIC) microscopy. Both improve contrast for specimens which add an optical delay but do not significantly absorb (known as phase objects). You do not need to know how these work, but you can read about them at:
https://www.olympus-lifescience.com/en/microscope-resource/primer/techniques/dic/dichome/
Note that, in both cases, the relationship between the actual phase and the intensity pattern we see is quite complicated and generally not reversible, i.e. we can’t figure out the actual value of the phase. So we sometimes refer to this as qualitative phase imaging.
The goal of Quantitative Phase Imaging (QPI) is to reconstruct the complex field (amplitude and phase) by encoding phase information in the intensity recorded by the camera in such a way that we can recover the value of the phase.
Let us define the 2D complex field at the sample as \(E_S(x,y)\) and the square modulus of this as the intensity \(I_S = |E_S|^2\). If we have no lens, and place the camera some distance \(z\) from the sample, then the field at the camera can be calculated using a free-space propagator such as the Fresnel propagator. (You should be familiar with this idea, but you don’t need to be able to reproduce it in the exam).

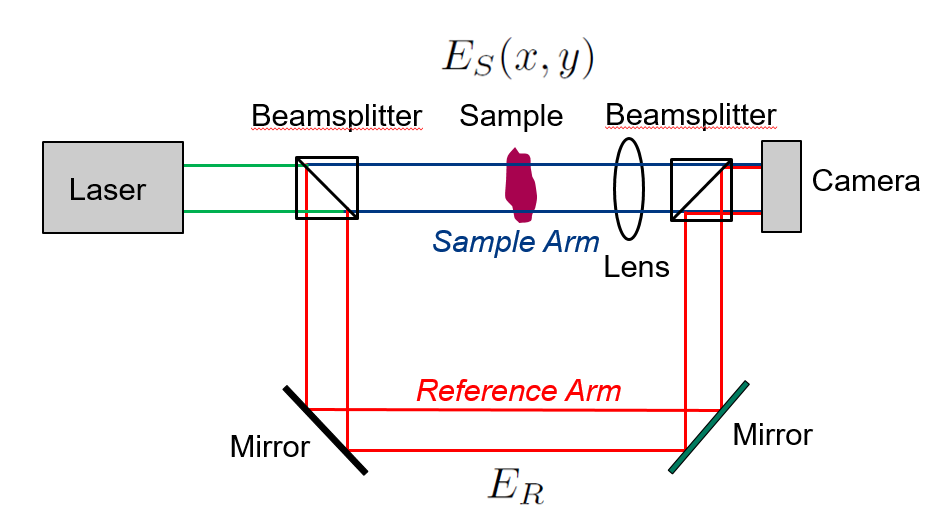
We introduce a second, reference, beam, of field \(E_R(x,y)\), which is coherent with the sample beam (i.e. we will see interference effects). Usually, this will be created using a beamsplitter and then recombined with the sample at the camera using another beamsplitter, as shown in Fig. 1. For simplicity we can assume it is a flat field with no spatial dependency, i.e. \(E_R(x,y) = E_R\). If the sample and reference fields coincide at the camera, then we have
\[E_{cam} = E_S(x,y) + E_R\]
The intensity at the camera is then: \[I_{cam} = |E_{cam}|^2 = I_S + I_R + E_R E_S^* + E_S E_R^*\]
where \(*\) denotes the complex conjugate. Note that this is a real quantity which, due to the last two terms (the cross-terms), will depend on the relative phase of \(E_R\) and \(E_S\) at each point on the camera. The third and fourth term are therefore an interferogram which depends on the complex value of \(E_S\). Since the reference field is simply a (known) constant, if we could isolate the fourth term then we have \(E_S\) which is complex and tells use the amplitude and phase at the camera. There are several different ways of isolating this term.
Now, if the sample is imaged onto the camera, this is then also the field at the sample (subject to any magnification and the effect of the PSF). If the sample is not imaged onto the sample, then we can use an appropriate free space propagator (usually the Fresnel propagator) to transform the field at the camera to the field at the sample.
Aside: We have made the simplification of ignoring the fact the the E field also varies in time, that is we should really write \(E(x,y,z,t) = |E|\cos(kx-\omega t) = \operatorname{Re}\{|E|e^{i[kx-\omega t]}\}\) where \(\omega\) is the angular frequency of light, related to the frequency \(\omega=2\pi f\), where \(f = c/\lambda\). If we follow this through we find that the time dependence cancels in the cross terms as it is the same for the reference and the sample beams - we are sensitive only to the difference in the path length. The time dependence is still present in the \(|E_S|^2\) and \(|E_R|^2\) terms, but as the frequency on light is much higher than the frequency bandwidth of any detector we might use, we essentially average over the sinusoidal time dependence, and again we don’t see it.
One method of isolating the \(E_S\) term is called phase shifting digital holography. We acquire several images with slightly different length reference arms. This introduces additional phase shifts (\(\phi\)) into the reference arm. This is normally achieved using a mirror mounted on a piezo actuator, replacing one of the mirrors in Fig. 1. We can write this as: \[E_R' = E_Re^{i \phi}\] There are a variety of algorithms for recovering the phase of \(E_S\) in this way. The classic method is four-step phase shifting; if we acquire four images with four different phase shifts of \(\theta = 0\), \(\theta = \pi/2\), \(\theta = \pi\), and \(\theta = 3\pi/4\) then the complex field is given by: \[E_S = \frac{1}{4E_R} [(I_0 - I_{\pi})] + i(I_{3\pi/2} - I_{\pi/2})]\]
We can then calculate the phase from this complex representation: \[\phi = \arctan \frac{I_{3\pi/2} - I_{\pi/2}}{I_0 - I_{\pi}}\]
There are other schemes involving fewer images, but they are generally either more sensitive to noise or small errors in the phase stepping or more computationally expensive.
By introducing a tilt into the reference beam, as shown in Fig. 2 it’s possible to recover the complex field without multiple phase-stepped images. First, note that tilting a beam with an angle of \(\theta\) is equivalent to adding a phase ramp of the form \(e^{i2\pi k x sin \theta}\). The total field at the camera is then:
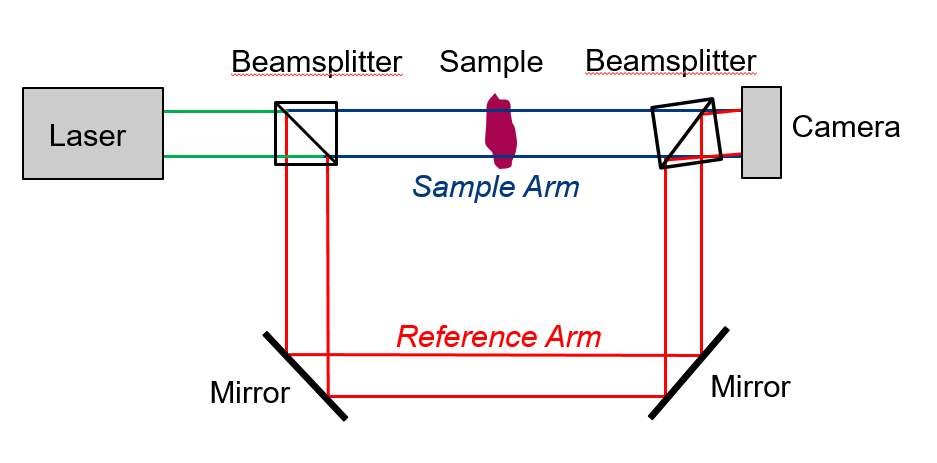
\[E_{cam} = E_Re^{i2\pi k x sin \theta} + E_S(x,y)\]
And hence the camera records intensity:
\[I_{cam} = I_R + I_S(x,y) + E_RE_S^*(x,y)e^{i2\pi k x sin \theta} + E_R^*E_S(x,y) e^{-i2\pi k x sin \theta}\]
We can now see that the components which depend on the complex field \(E_S\), rather than its square (\(I_S\)), are modulated by the exponential terms, and so in Fourier space are shifted compared with the \(I_R\) and \(I_S\) terms.
To recover the complex field, \(E_S\), we extract the region in Fourier space which is occupied by one of the modulated components and shift it to be centred on zero, before inverse Fourier transforming back to real space. This is equivalent to demodulating around the carrier frequency which comes from the tilted reference beam. The effect is that the resulting image is complex, and we can now directly extract the amplitude and phase. This procedure is shown in Fig. 3.
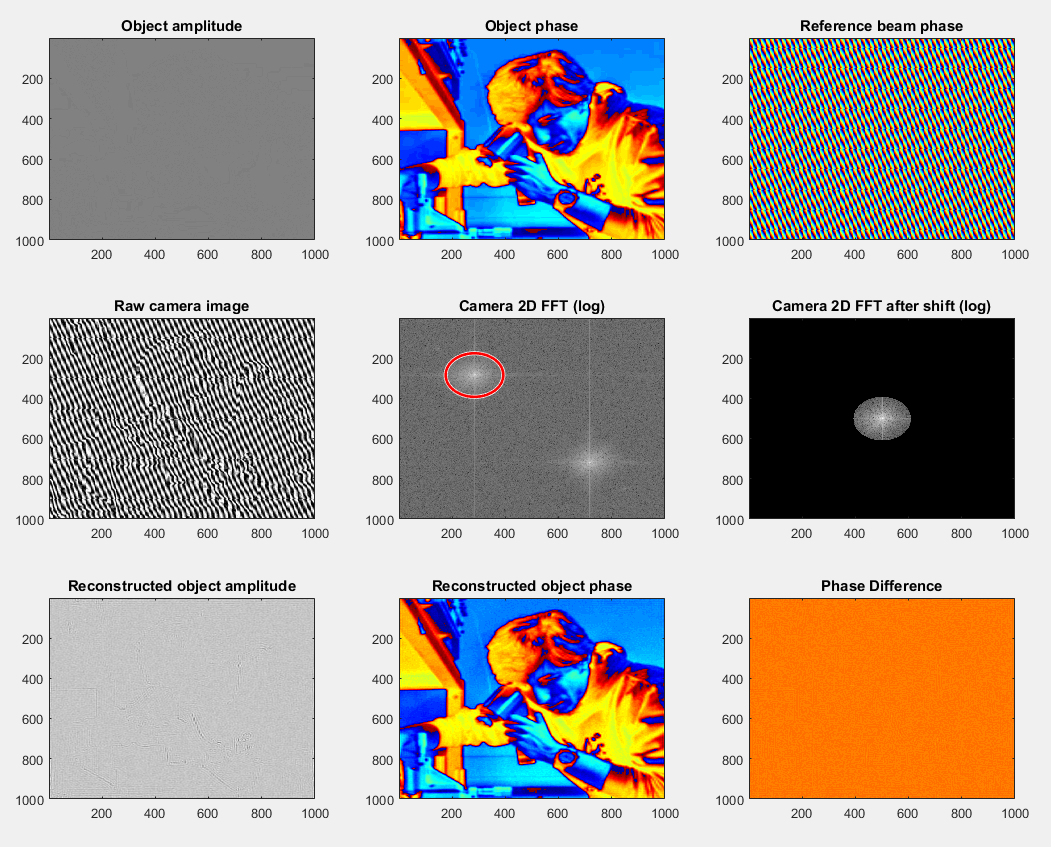
Off-axis holography allows the phase to be recovered from a single image, so it is fast. The processing is also relatively simple, requiring only Fourier transforms. However, the modulated component must be shifted sufficiently far in Fourier space for there to be no overlap with high spatial frequencies coming directly from the sample (In the \(I_S\) term.). Therefore one needs more pixels on the camera to achieve Nyquist sampling of the spatial frequencies present in the sample field (or, if insufficient pixels are available or the tilt angle cannot be increased sufficiently, to limit the spatial frequencies coming from the sample by reducing the numerical aperture). We also have to ensure that there is no vibration which changes the relative path length (sample and reference), or our phase values will vary in time.
In in-line holography (sometimes known as on-axis or Gabor holography), instead of using a separate reference beam, we rely on interference between light scattered from the sample and the illumination beam itself. The camera is placed a short distance behind the sample, and generally no lens is used. This results in a an interference pattern on the camera. We can then try to estimate the complex field at the sample plane using a technique called back propagation. Both planar and point source illumination geometries can be used, as shown in Fig. 4

We first calculate the reference field at the camera plane. We then calculate the conjugate of this field, meaning we reverse its direction. We then multiply this conjugate field by the image and numerically propagate it back to the sample plane. This is essentially a digital equivalent of the very earliest forms of holography, in which the interference a pattern between the object and a reference beam was recorded on photographic film. Shining light back through the film then produces a hologram.
A problem with in-line holography is that the reconstructed field at the sample is corrupted by zero order diffraction and the ‘twin image’. The twin image is due to an ambiguity in the reconstruction The former can be dealt with by subtracting the mean of the hologram. The twin image problem is more troublesome, and can prevent quantitative phase imaging. There are a number of approaches which attempt to reduce the twin image problem, and these do allow effective recovery of the phase. Choosing a point source geometry with sufficient sample to detector distance means that the twin image is heavily blurred, minimising its contribution. There are also numerical approaches but they are iterative and slow and generally require some prior information about the sample. Further discussion of these methods are beyond the scope of this lecture, but there is a large amount of literature on the subject, and it is an active research topic.
In-line holography is optically simple, requiring only a light source (which can be an LED) and a camera. It is less sensitive to disturbance or vibrations, since these are common to both beams. This makes it ideal for portable, low cost imaging applications, especially as there is no need for a lens. A partially spatially coherent source can be used for off-axis holography, since interference only takes places over a relatively small spatial area. The temporal coherence length can also be very short, since there is little path length difference between the deflected and un-deflected light. A pinhole of 50-100 microns placed in front of a high power LED can work well as a source. This makes inline holography attractive for low-cost microscopy.
However, since no lens is used, the pixel size of the camera directly limits the resolution. There is the ’twin image problem’ which requires an iterative phase recovery algorithm, making this a slow approach to quantitative phase imaging.
Contrast: As for conventional phase contrast
imaging, QPI allows samples which do not absorb or scatter strongly
enough to be seen in intensity images to be viewed.
Thickness measurements: Since the phase delay depends
on the thickness of the samples (assuming constant refractive index)
then the phase measurements can be used to infer the thickness of the
sample at each \((x,y)\) point and
hence recover a 3D representation of the sample.
Numerical Refocusing: Once the complex field is known
as some distance from the sample, we can adjust the focus position
numerically using the Fresnel propagator to compute the field at any
other distance. This allows post-acquisition adjustments in the focus
position, or acquisition of extended depth of field images, with no
physical turning of knob.
Index of Refraction Measurements: The
phase changes induced by a sample depending on the optical path, \(D,\) length through the sample. \(D = nL\) where \(L\) is the physical thickness and \(n\) is the refractive index. Hence if the
physical thickness of an object is known then phase measurements can be
used to recover the refractive index (or rather than line integral
through the sample).