The notes below are a summary of the key points needed for the exam. For more details and background they should be read in conjunction with linked documents, papers or websites and the general reading:
Olympus Microcsopy Resource Centre: https://www.olympus-lifescience.com/en/microscope-resource/
Nikon MicroscopyU https://www.microscopyu.com/
The resolution of a microscope is fundamentally limited by diffraction. The image of an infinitesimal point will be ‘blurred’ by the system’s point spread function (PSF). In the spatial frequency domain we can think of this as an attenuation of higher spatial frequency components, described by the modulation transfer function (MTF). These terms are defined more rigorously later.
The finite resolution of a microscope can be understood in terms of the spatial frequencies which are passed from the object to the image plane. Roughly speaking, to reconstruct a feature of a certain small size, our microscope must transmit spatial frequencies on the order of the feature’s size.
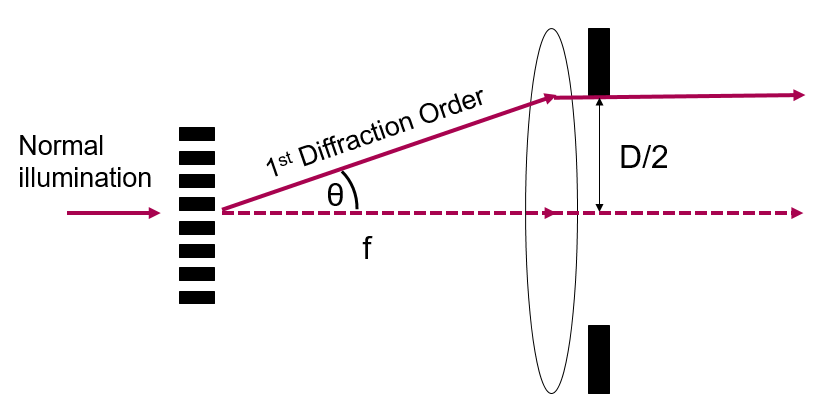
To understand what happens to a given spatial frequency, consider a fine sinusoidal periodic structure in the object, as shown in Fig. 1. The structures are separated by a distance \(d\) and so have spatial frequency \(1/d\). This structure acts like a diffraction grating, and hence if we consider only the first diffraction order, normally incident light of wavelength \(\lambda\) will be diffracted by an angle \(\theta\), where:
\[d \sin \theta = \lambda\]

In order to capture a spatial frequency of \(1/d\), our lens must collect light diffracted at an angle \(\theta\). If the lens is at a focal length of \(f\), then it must have an aperture diameter, \(D\), such that: \[\frac{D}{2f} = \sin \theta.\]
We define the numerical aperture of our microscope objective as \[NA = n \sin \theta = D / 2f,\] where \(n\) is the refractive index of the medium between the sample and the objective. In general this is air, and so \(n = 1\), but in oil immersion objectives it can be higher.
Hence, for our microscope to capture a spatial frequency \(1/d\), and resolve objects of size \(d\), we have: \[d = \frac{\lambda}{NA}\]
However, this assumes we illuminate the sample with plane waves. Say now we illuminate from all angles using a condenser with the same NA as the objective. Now, as shown in Fig 2, we can collect spatial frequencies which have been diffracted through \(2 \theta\), and hence which are twice as high. So our final formula becomes:
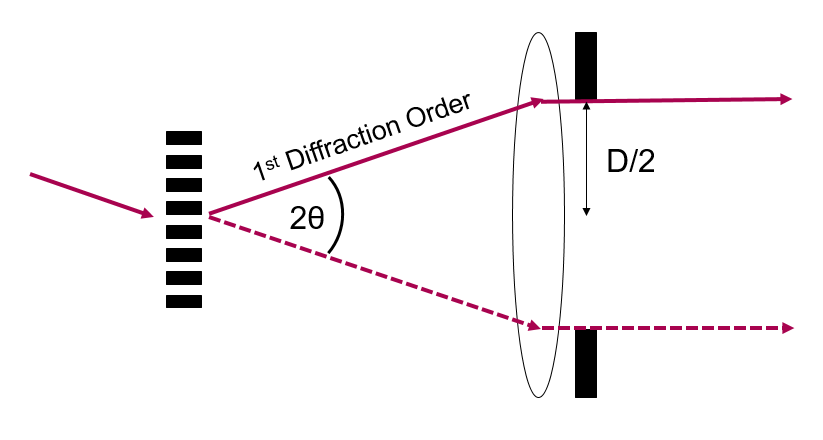
\[d_{abbe} = \frac{\lambda}{2NA}\]
This is known as the Abbe limit, it tells us the maximum spatial frequency we can collect, known as the cut-off frequency. Alternatively it tells us the objective NA we require in order to capture features with a certain spatial frequency. However, it is not necessarily the best way to determine if we can actually resolve those objects, as we are ignoring the extent to which these frequencies are attenuated through diffraction.
For an incoherent imaging system, an infinitesimally small point of intensity at the object plane will be spread out at the image plane. The ‘spreading out’ is defined by the incoherent point spread function (PSF). Ideally the PSF is shift invariant, i.e. it is the same for all positions in the object/image, but in practice this is never quite the case. The PSF is a 2D function, but when it is radially symmetric we often plot a 1D profile through it.
We can consider any intensity distribution at the object plane to be a super-position of an arbitrarily large number of infinitesimal points. Hence, the image can be expressed as a summation of PSFs, one for each point on the object. Mathematically, we express this as a convolution.
Consider an object \(O(u,v)\), where \(u\) and \(v\) are the lateral co-ordinates at the object plane. For some perfect (and physically impossible) imaging system (i.e. one which exactly reproduces the object), we can write the image \(I(x_0,y_0)\) as
\[I(x,y) = \int \int O(u,v) \delta(x_0 -u, y_0 - u)~du~dv,\] where \(\delta\) is the delta function. For any real system we replace this delta function with a finite point spread function \(PSF(x_i,y_i)\), and the image is then similarly given by:
\[I(x_0,y_0) = \int \int O(u,v) PSF(x_i - u,y_i - v)~du~dv\]
or \[I= O\ast PSF\] where \(*\) represents convolution.
In the spatial frequency domain, the analogue of the PSF is the modulation transfer function, MTF (i.e. the 2D MTF is the 2D Fourier transform of the 2D PSF).
Recall from Fourier theory that a convolution in the spatial domain is equivalent to a multiplication in the spatial frequency domain. The MTF can be thought of a weighting function by which we attenuate each spatial frequency (i.e. it is a function telling us what fraction of each frequency of modulation the system is able to transfer.).
We also define the optical transfer function (OTF). This contains the same information as the MTF but also describes the phase delay that different spatial frequency components receive. Usually the OTF is expressed as a complex number, and the MTF is then the magnitude/modulus of the OTF.
We further define the pupil function, which tells us how the amplitude of light passing through different points of the aperture of the microscope is attenuated (as well as any phase change). For an ideal microscope with a circular aperture, this is just a circle.
The pupil plane is a Fourier plane with respect to the object plane. So we can think of this as effectively a ‘spatial frequency plane’, the size of the pupil determines the cut-off spatial frequency (refer to the discussion earlier).
The PSF is the absolute square of the Fourier transform of the pupil function. This means, from Fourier theory, that the OTF is the autocorrelation of the pupil function, and the MTF is the magnitude of this. This is a slightly confusing point and requires some thought.
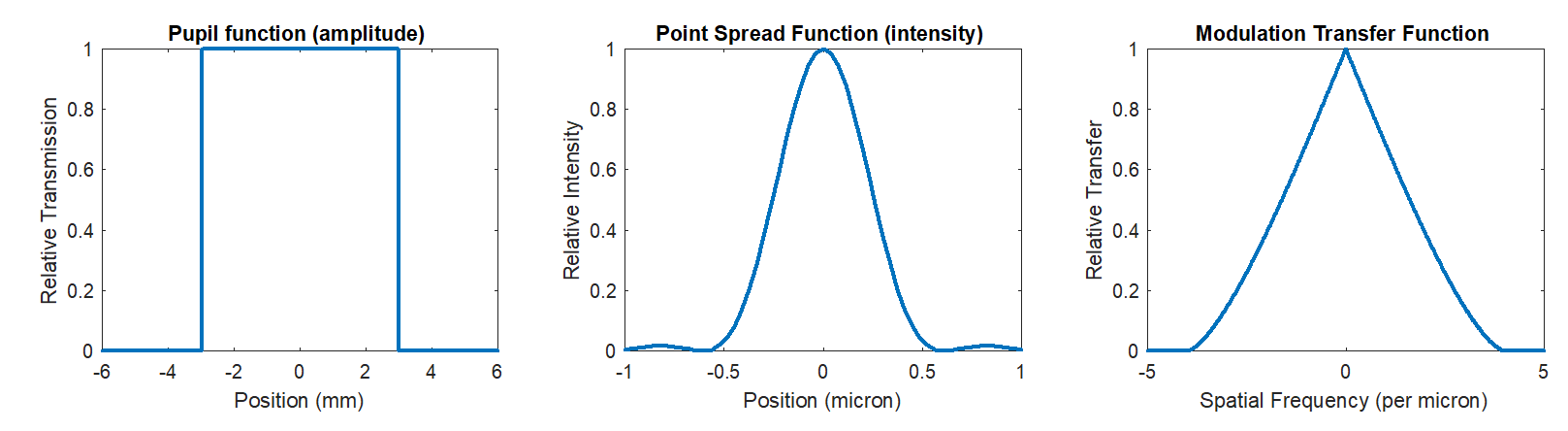
An example of a pupil function and the corresponding PSF and MTF are shown in Fig. 3. Matlab code to generate these plots is on Moodle. We can see from the MTF plot that a microscope is a low-pass filtering system with a cut-off frequency.
Some caution is needed here, these are slices through 2D functions, not 1D functions. The slice through the MTF is not simply the autocorrelation of the slice through the pupil function, we must perform the 2D autocorrelation on the 2D pupil function and then take the slice. Otherwise the MTF would be a triangular function (the autocorrelation of a ‘rect’ function) whereas careful observation will reveal a slight curvature.
A final subtlety is that, again, a 1D slice thought the 2D MTF is NOT the 1D Fourier transform of a 1D profile through the 2D PSF (You may need to convince yourself this is the case). The 1D Fourier transform of the MTF is actually the line spread funtion (LSF), which describes how a line, rather than a point, spreads. It is related to the PSF via the Abel transform. An excellent tutorial discussing this is available here:
https://www.dspguide.com/ch25/1.htm
The incoherent point spread function is an intensity point spread function, i.e. it allows the intensity value at the camera plane to be written in terms of the intensity values at the object plane. This is possible because an incoherent microscope is linear in intensity.
We cannot define an intensity point spread function for a coherent imaging system due to the presence of interference. An coherent microscopy is linear in electric field, not the intensity. The image therefore depends on the phase of the object.
Instead of the incoherent PSF we must define an amplitude point spread function, also known as the coherent point spread function or cPSF, which acts on the complex electric field. Once we have convolved the (complex) object with this amplitude point spread function we can then take the square modulus to determine the resulting intensity on the camera. Note that this is emphatically not the same as convolving the object plane intensity with the square of the amplitude PSF.
A detailed (and excellent) discussion on this and the ways can define resolution for coherent imaging systems was published in Nature Photonics in 2016:
https://www.nature.com/articles/nphoton.2015.279
For a perfect, diffraction-limited objective, the corresponding PSF is an Airy pattern, as shown in Fig. 4. The left version of the image has been scaled to make the ringing clearer.
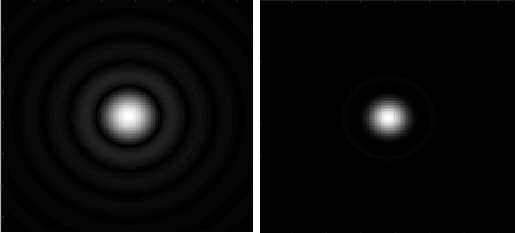
This is in fact the 2D Fourier transform of a circular aperture, as discussed above. Mathematically it is given by \[{I = I_0\Big(\frac{2J_1(r)}{r}\Big)},\] where \(I_0\) is the maximum intensity at the centre of the pattern, \(J_1\) is a 1st order Bessel function of the first kind, and \(r\) is the radial co-ordinate. The first minimum occurs at a distance of: \[r = 0.61 \lambda/NA\]
The central disk inside this radius is called the Airy disc.
Resolution is not unambiguously defined. Informally, it is usually taken to mean the ability to tell whether two point objects are actually two separate objects, but in practice this depends on things other than the MTF of the microscope (such as noise levels). To quantify resolution we require a formal definition of when two points can be resolved. These are illustrated in Fig 5.
The Rayleigh criterion states that two points can be distinguished when the peak of the Airy pattern from one of the points is aligned with the first minimum of the Airy pattern from the second. For an ideal microscope with a circular aperture, this comes out to be: \[d_{Rayleigh} = 0.61 \frac{\lambda}{NA}\]
The Sparrow criterion, says instead that the two objects can be resolved when the sum of their intensity patterns no longer has a dip (see diagram). This occurs at
\[d_{Sparrow} = 0.47 \frac{\lambda}{2 NA}\]
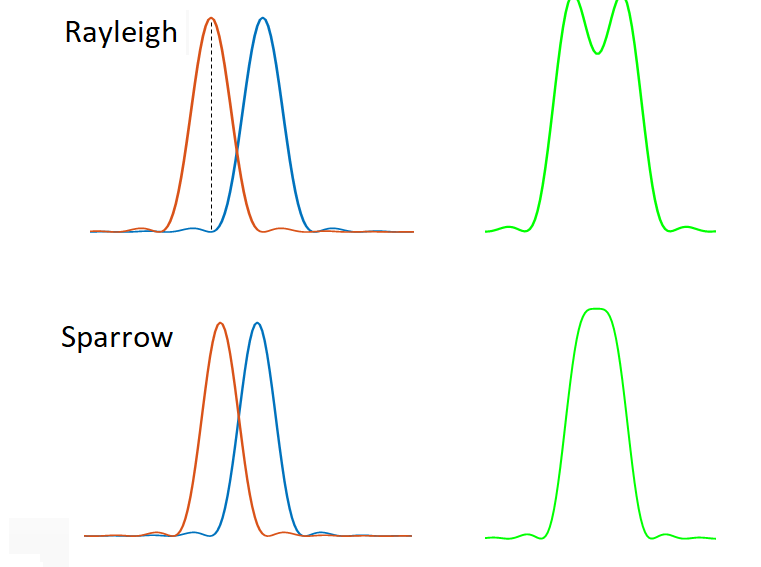
So the Sparrow limit gives a smaller (better) value for resolution than either the Rayleigh or Abbe limits. In all cases, the rule of thumb is that the resolution is of order \(\lambda /2NA\).
All the resolution considerations above do not affect our choice of magnification. However, when a pixelated detector, such as a camera is used, we must also consider the effect of the pixelation on the resolution. Let’s define:
Pixel pitch: The spacing between the centres of the pixels.
Pixel size: The size of the active area of the pixel.
The fill factor: Ratio of the pixel size to the pixel pitch.
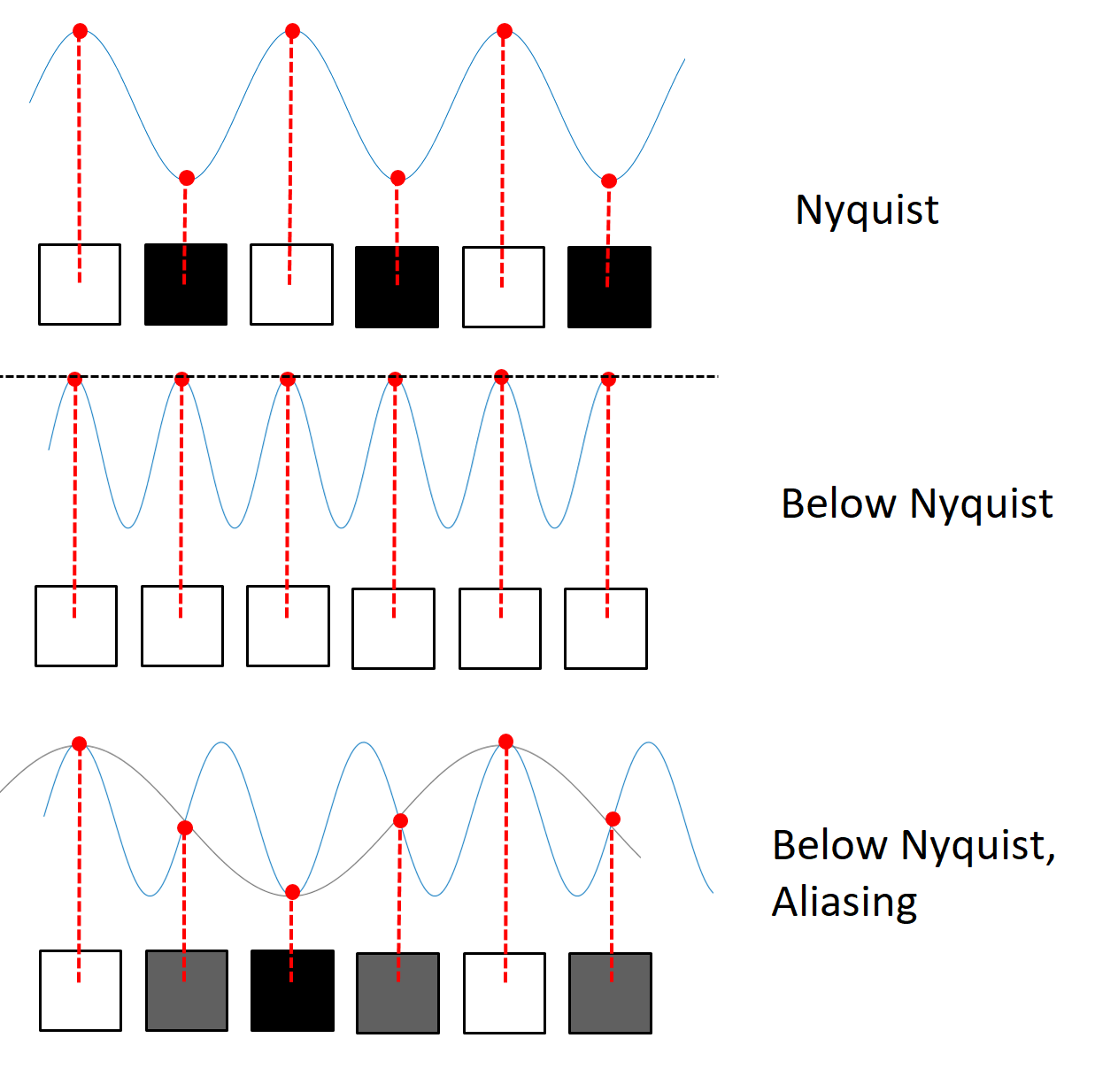
From the point of view of sampling theory, it is the pixel pitch which matters. Nyquist theory tells us that the sampling pitch must be half the spacing corresponding to the highest spatial frequency in order to sample that frequency without aliasing. (Or equivalently, the sampling frequency must be twice the maximum spatial frequency we wish to sample.)
This does not trivially relate to the resolution criteria defined above, but the common rule of thumb is to assume we require a pixel pitch which is twice the diffraction limited resolution as magnified onto the camera. For example, if our resolution is 1 m and we have a 40X magnification, then we require a pixel pitch of less than 20 m.
Aside: There is a secondary effect due to the fact that each pixel integrates over an area. This reduces the contrast of higher spatial frequencies, and so may reduced the signal to noise ratio for the spatial frequencies to such a point that they cannot be observed, but this is different from the sampling theory.
In the (usually avoided) case where the pixel pitch is too large to sample the highest spatial frequency reaching the camera, then the resolution is pixel-limited. Pixel limited resolution is shift variant - the ability to resolve two objects depends on their position relative to the pixel grid. So we cannot define a shift invariant point spread function or define an unambiguous MTF.