The notes below are a summary of the key points needed for the exam. For more details and background they should be read in conjunction with linked documents, papers or websites and the general reading:
Olympus Microcsopy Resource Centre: https://www.olympus-lifescience.com/en/microscope-resource/
Nikon MicroscopyU https://www.microscopyu.com/
In this section we will review some fundamental concepts from geometrical optics which will already be familiar to most, and begin thinking about the design of a simple microscope.
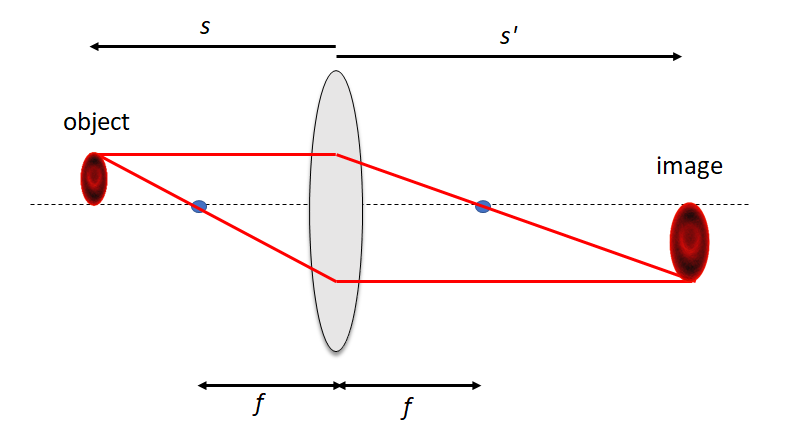
A lens is piece of glass or plastic with one or both of its surfaces curved in such a way as to cause light rays to converge or diverge due to refraction. In what is follows, we use the thin lens approximation, which ignores the thickness of the lens. In which case, the locations of the object (\(s\)) and image (\(s'\)), see Fig. 1, for a lens are linked to the focal length of the lens, \(f\), by the lens equation:
\[\frac{1}{f} = \frac{1}{s} + \frac{1}{s'}\] If we have a lens of focal length \(f\), and we place an object a distance of \(s\) one side of the lens, we obtain an image a distance \(s'\) the other side of the lens.
Note that \(s\) and \(s'\) are both measured from the lens outwards (i.e. in a system such as that shown in Fig. 1, where the object is to the left of the lens, \(s\) is measured from right to left and \(s'\) is measured from left to right.) An object to the left of the lens has a positive \(s\) and an image to the right of the lens has a positive \(s'\). This is called the Gaussian co-ordinate system. An alternative system, the Cartesian co-ordinate system, measures everything from left to right which is useful when dealing with some kinds of systems. In this system, the lens equation would have a minus sign before the \(1/s'\) term.
The focal length \(f\) is fixed for a given lens, it depends on the curvature of its surface according to the lens makers’ equation: \[\frac{1}{f} =(n-1)\bigg(\frac{1}{r_1}-\frac{1}{r_2} \bigg)\]
where \(r_1\) is the radius of curvature of the first surface of the lens, \(r_2\) is the radius of curvature of the second surface, and \(n\) is the refractive index of the lens material.

A real image is obtained for \(s > f\). Otherwise there will be no real image, and \(s'\) is negative, with rays appearing to diverge from a virtual image at \(s'\) (i.e. on the left side of the lens, as drawn).
The linear magnification, the ratio of the size of the image to the size of the object, \(M\), is given by \[M = -\frac{s'}{s}\]
The minus sign tells us that the image is inverted.
Let’s consider the eye to be a simple imaging system, consisting of a thin converging lens (eye lens and cornea) and a screen (the retina). The distance from the lens to the retina is fixed, but the focal length of the thin lens, \(f\), can be changed by the muscles in the eye (known as accommodation). If the object has size \(y\) then the size of the image on the retina, \(y'\), depends on the object’s distance from the lens, \(s\) as shown in Figure 2.
Under the paraxial approximation, an object of size \(y\) subtends an angle \(\theta = y/s\). In principle we can make an object as big as we like by bringing it arbitrarily close the lens. However, this requires \(f\) to be adjusted, and there is a limit to how far the eye can accommodate. The closest an object can be brought and still focused on the retina is called the near point of the eye, and is comfortably around \(x_{np} = 25\) cm for a healthy eye. The angle subtended by the object is approximately \(y/x_{np}\).
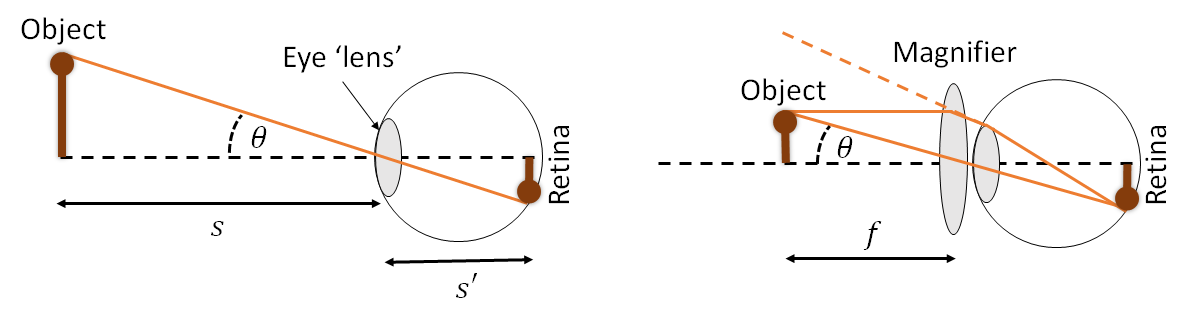
A simple magnifier is a converging lens placed in front of the eye lens, with an object we wish to view placed at the focal length of the lens. The lens makes the object appear as though it is at infinity. The eye can then fully relax, as it is when accommodated to view objects at infinity, but the image size on the retina is the same as if the object was placed at \(f\). That is to say that the angle subtended by the object, \(\theta\) is the same. Since this angle is now given by \(y/f\), we can write the angular magnification of the magnifier as \[M = \frac{x_{np}}{f}\]
This is also the ratio of the size of the object on the retina when viewed through the magnifying glass, at a distance of \(f\), compared to the size if we viewed it without the magnifying glass, when we would need to move the object out to the near point, \(x_{np}\)
Consider an ideal thin lens of focal length, \(f\). Recall that an object at infinity is imaged a distance \(f\) behind the lens. If an object is placed a distance \(s\) in front of the lens, it will be imaged a distance \(s'\) behind the lens, where \[1/f = 1/s + 1/s',\] with a linear magnification, \(M = -s'/s\)
For a thin aberration-free lens in geometrical optics we can obtain arbitrarily high magnification through our choice of \(s\), and if we place a camera at the position of the image, we have a microscope.
More traditional compound microscopes, where we can look directly at the image, require an extra element called an eye-piece. This is because the image formed by the objective is still quite small, to get it to fill a decent portion of the eye’s angular field of view we would have to get very close to it, closer than the near point. The job of the eyepiece is to take the image and make it appear as though it is at infinity, allowing our eyes to relax - the same job as the simple magnifier. This is done by placing the eyepiece so that the image of the object is at its focal length, \(f_e\). This is shown in Figure 3
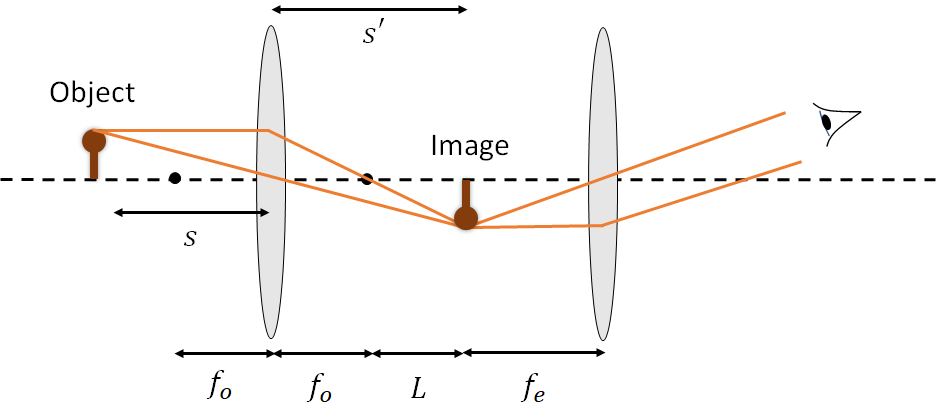
For the objective, of focal length \(f_o\), the linear magnification is given by \(-s'/s\). However, we may also write this magnification as approximately: \[M = -\frac{L}{f_o}\] where \(L\) is the distance between the focal points of the objective and the eye-piece. This is called the tube length. This approximation is valid because we typically want a large magnification, and so \(s' \gg s\). This means that the object is quite close to the focal point, i.e. \(s \approx f_o\), and \(L\gg f_o\) such that \(L \approx s'\).
The magnification of the entire microscope includes the angular magnification of the eyepiece (\(x_{np}/f_e\)) and so the total magnification is:
\[M = -\frac{L}{f_o}\frac{x_{np}}{f_e}\]
In practice, we find the resolution of this microscope would be very poor. We will see shortly that the ultimate limit on resolution is given by the numerical aperture of the lens. However, in practice, as we increase the numerical aperture of simple spherical lens, we find that the image resolution is instead limited by optical aberrations. Using an aspheric lens it’s possible to minimise aberrations on-axis, but it isn’t possible to design a single surface lens which provides high resolution across a meaningful field of view.
Practical objectives are multi-element, i.e. they contain multiple surfaces which are optimised to minimise aberrations. For colour, or multi-wavelength imaging, they must also be achromatic (i.e. different wavelengths are focused to the same point) and flat-field, meaning that the in-focus image is formed on a plane, and not a curved surface. Generally, the more you are willing to pay, the better these correction will be. There are a bizarre (for historical reasons) set of names for the different levels of correction available, which you can read all about here:
https://www.olympus-lifescience.com/en/microscope-resource/primer/anatomy/specifications/
An important distinction is between finite conjugate and infinite conjugate objectives:
Finite Conjugate: An objective designed to form an image directly on the camera. Objectives are designed for the camera to be placed at a specific distance (\(s'\)), usually either 160 mm (DIN standard) or 180 mm (RIS standard). Of course, you can form an image at different distances, providing you also change the distance to the object, \(s\), but the corrections won’t be as good. Objectives are specified in terms of their magnification, such as x10, or x40, and you only obtain this magnification with the camera placed at the correct distance. For direct visualisation of the image, an eyepiece is also required. This also has a magnification specified, and the total magnification is given by the product of the two.
Infinite Conjugate: An infinite conjugate microscope objective is designed to be used with the object placed at the focal length, \(f\), and so form an image at infinity. They therefore require a second lens, known as tube lens, to form an image on the camera. These objectives are again specified by magnification, but now this depends on using a tube lens of the specified focal length. There is also usually a range of tube lengths (distance between the objective and the tube lens) which are recommended. Some infinite conjugate objectives are designed to work with a specific tube lens in order for the correct aberration correction to be achieved.
Advantages of infinite conjugate objectives: Elements with optical thickness (such as filters and beamsplitters) can be placed in the optical path without affecting the magnification. Infinite conjugate objectives are also needed in scanning laser systems such as confocal microscopes (more on this in lecture 3).
The condenser is the element used to illuminate the sample. The condenser has an important role to play in resolution, as discussed later, the theoretical resolution of a transmission microscope cannot be achieved if the numerical aperture does not match the numerical aperture of the objective. In some configurations, illumination light is sent through the objective, in which case the objective and the condenser are one and the same.
To observe features in a sample there must be some difference in intensity or colour between those features and other areas of the image. The contrast depends not only on the sample, but on the design of the microscope and illumination.
Brightfield: Most simple microscopes operative in bright field transmission mode. The sample is illuminated from the back, and we obtain contrast because the sample absorbs or (to a lesser extent) scatters light. Of course the sample must be at least partly transparent, or we simply obtain a silhouette. This type of microscope therefore cannot image thick samples. Samples are often stained in order to selectively increase absorption. A common staining protocol used in histology is H&E (Hematoxylin and Eosin) which stains components of tissue various shades of blue, violet and red.
Darkfield: When absorption cannot provide sufficient contrast, particularly for unstained samples (e.g. live samples), darkfield microscopy may sometimes be used. In this case, the sample is illuminated at a high angle of incidence, such that undeflected light cannot reach the objective. We therefore only see light which is scattered by the sample, and the background is dark.
Read more:
https://www.olympus-lifescience.com/en/microscope-resource/primer/techniques/darkfieldindex
Fluorescence Microscopy: When certain molecules, called fluorophores, absorb light of certain wavelength, they re-emit light at a longer wavelength. The difference between the excitation and emission wavelengths is called the Stoke’s shift. Physically, an incident photon excites an electron to a higher energy level. It then relaxes to a slightly lower level via internal energy transfer processes, before re-emitting and dropping back down to the original level. Since the drop is now a smaller change in energy, the emitted photon is lower energy and so has a longer wavelength.
When a sample is naturally fluorescent, we call this intrinsic or autofluorescence. More often, we apply fluorescent stains or generically engineer an organism to contain fluorescent proteins.
To image fluorescene we introduce a fluorecence filter set. The excitation filter ensures we illuminate the sample only with the correct excitation wavelength, and the emission filter selects only the fluorescent emission. Without the use of filters, the fluorescence emissions would be drowned out by the excitation light hitting the camera.
The direction of the emitted photon is random and doesn’t depend on the direction the excitation came from. So there is no distinction between bright-field and dark-field imaging. Fluorescence microscopy is often performed in epi configuration, meaning that the sample is excited from the sample side as it is imaged, via the same objective. A dichroic mirror, which reflects light below a certain threshold wavelength and transmits light above this threshold (or vice versa) is then used to separate the excitation and emission optical paths.
Read more:
https://www.olympus-lifescience.com/en/microscope-resource/primer/techniques/fluorescence/fluorhome
Phase contrast microscopy will be discussed in Lecture 3.