In this chapter we will apply the principles of geometrical optics to the study of three instruments: a simple magnifier, a microscope and a refracting telescope.

The Simple Magnifier

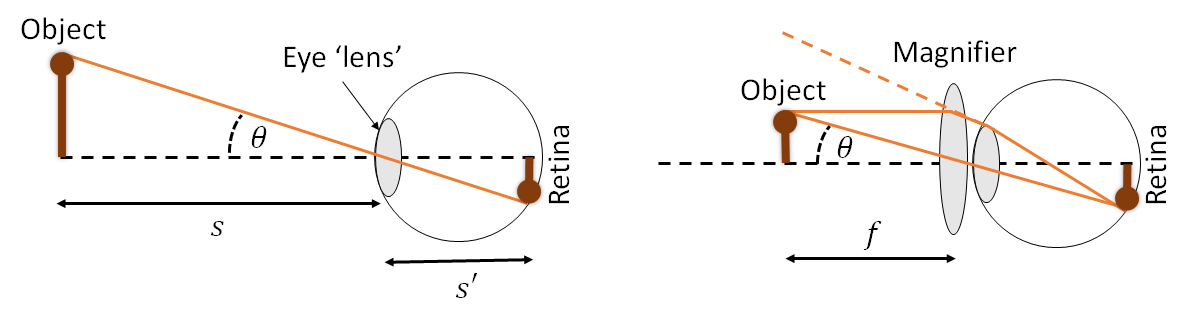
Let’s consider the eye to be a simple system, consisting of a thin converging lens (eye lens + cornea) and a screen (the retina). The distance from the lens to the retina is fixed, but the focal length of the thin lens, \(f\), can be changed by the muscles in the eye (known as accommodation). If the object has size \(y\) then the size of the image on the retina, \(y'\), depends on the object’s distance from the lens, \(s\) as shown in Figure 1.

Under the paraxial approximation, an object of size \(y\) subtends an angle \(\theta = y/s\). In principle we can make an object as big as we like by bringing it arbitrarily close the lens. However, this requires \(f\) to be adjusted, and there is a limit to how far the eye can accommodate. The closest an object can be brought and still focused on the retina is called the near point, and is comfortably around \(x_{np} = 25\) cm for a healthy eye. The angle subtended by the object is approximately \(y/x_{np}\).

A simple magnifier is a converging lens placed in front of the eye lens, with an object we wish to view placed at the focal length of the lens. The lens makes the object appear as though it is at infinity. The eye can then view the object relaxed, as though it is at infinity, but the image size on the retina is the same as if the object was placed at \(f\). That is to say that the angle subtended by the object, \(\theta\) is the same. Since this angle is now given by \(y/f\), we can write the angular magnification of the magnifier as \[M = \frac{x_{np}}{f}\]

This is also the ratio of the size of the object on the retina when viewed through the magnifying glass, at a distance of \(f\), compared to the size if we viewed it without the magnifying glass, when we would need to move the object out to the near point, \(x_{np}\)

The Microscope

We have seen in Chapter 2 that we can use a simple lens to magnify an object. We call a lens used in this way an objective. If we place a camera where the image is formed, then we have a microscope. This is how simple digital microscopes work, although the thin lens is replaced with a microscope objective which is optimised for resolution and image quality (which is beyond the scope of this course).

More traditional compound microscopes, where we can look directly at the image, require an extra element called an eye-piece. This is because the image formed by the objective is still quite small, to get it to fill a decent portion of the eye’s angular field of view we would have to get very close to it, closer than our eyes can focus. The job of the eyepiece is to take the image and make it appear as though it is at infinity, allowing our eyes to relax - the same job as the simple magnifier. This is done by placing the eyepiece so that the image of the object is at its focal length, \(f_e\). This is shown in Figure 2

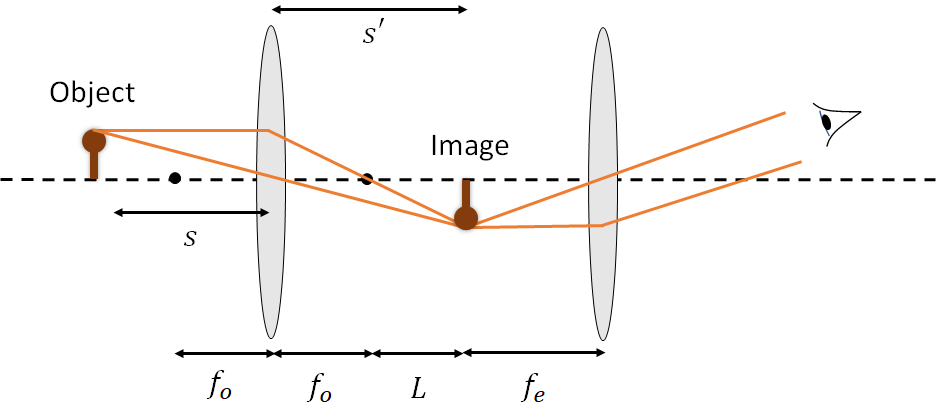
For the objective, of focal length \(f_o\), the linear magnification is given by \(-s'/s\). However, we may also write this magnification as approximately: \[M = -\frac{L}{f_o}\] where \(L\) is the distance between the focal points of the objective and the eye-piece. This is called the tube length. This approximation is valid because we typically want a large magnification, and so \(s' \gg s\). This means that the object is quite close to the focal point, i.e. \(s \approx f_o\), and \(L\gg f_o\) such that \(L \approx s'\).

The magnification of the entire microscope includes the angular magnification of the eyepiece (\(x_{np}/f_e\)) and so the total magnification is:

The Telescope

A telescope is designed to take an object at infinity (or very far away) and create an image of it at the focus of an eyepiece, which then allows us to view the object. The effect is to increase the angle subtended by the object (i.e. angular magnification). This is shown in Figure 3.

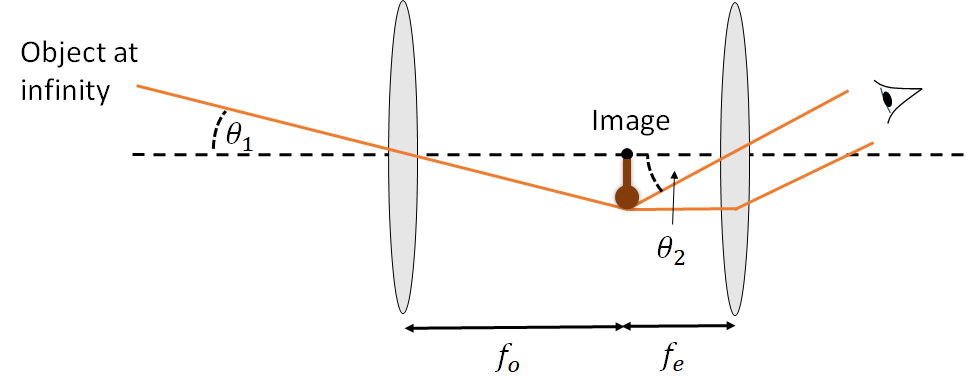
We define the magnification of the telescope as the ratio of the two angles subtended, \(\theta_1\) and \(\theta_2\), which gives:

Notice that this is angular magnification. In a microscope we have linear magnification due to the objective, i.e. we create a magnified image of the object. We then use an eypepiece for angular magnification of this image. In a telescope, at no point do we create an image of the object which is larger than the object, or this would require astronomical telescopes to be somewhat larger than practical.