Waves are an important phenomenon in physics, and one that you will encounter many times in your studies. Waves transport energy (and momentum) without transporting matter. Some waves travel through media (such as air) while others (such as electromagnetic waves) can travel through a vacuum. In the this section we will define some basic wave concepts and understand the idea of the wave equation, a differential equation describing wave motion.

Wave Motion

We start by considering a pulse travelling along a slinky string. We can generate this by oscillating one end of the slinky string. The wave pulse moves along the string, perpendicular to the driving oscillation. We refer to this as a transverse wave.

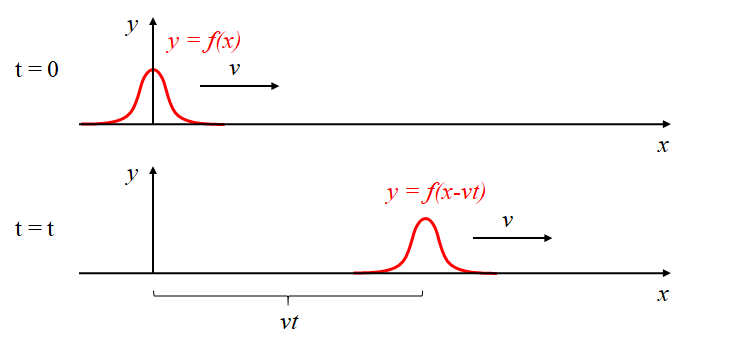
Let’s label the axis along the slinky as \(x\) and the axis on which we drive the oscillation as \(y\). We can then describe the displacement of any point along the slinky at some point in time by some function \(f(x)\) such that displacement, \(y\), is given by \(y = f(x)\).

If we have a wave motion then this pattern of displacement is moving along the slinky to the right with some speed \(v\). At time \(t\) the wave is then described by \[y = f(x - vt).\]

We can understand this by using the ideas of frames of reference introduced in special relativity. If we consider a frame of reference \(S\) attached to the crest of the wave, which has the form \(f(x)\) moving with speed \(v\) along the x-axis, then we can use the Galilean transformation \(x' = x-vt\) to immediately see that the wave appears to be \(f(x-vt)\) in a frame of reference where the wave is moving at speed \(v\). Check that you intuitively understand why this has a \(-vt\) and not a \(+vt\) when the wave is moving along the positive \(x\)-direction.

Transverse and Longitudinal Waves

The type of wave we discussed on the slinky spring is a transverse wave - the oscillation is perpendicular to the direction of wave propagation. The alternative is a longitudinal wave, in which the oscillation and the wave motion are along the same axis. Sound is a longitudinal wave, the air molecules oscillate to form compressions and expansions along the direction the wave is travelling. Light is a transverse wave, oscillations in the electric/magnetic fields are in the perpendicular direction - more on this later.

The Wave Equation

The wave equation is a general equation which has a huge range of applications across physics.

This is a second order partial differential equation in both space \(x\) and time \(t\). Strictly this is the 1D wave equation, since it has no dependence on the two other spatial co-ordinates, and we can write a similar equation in 3D. The exact meaning of \(y\) depends on the specifics of the wave.

An important property of the wave equation is that it is satisfied by any function of the form \(f(x) = x-vt\) (i.e. a travelling wave). We can verify this as follows.

Take some function \(y = f(x-vt)\). To simplify the maths, we will write \(\alpha = x-vt\); note that \(\alpha\) is therefore a function of \(x\) and \(t\), i.e. it is a function of the things we want to take the derivative with respect to.

We can then compute the LHS of the wave equation. Begin with taking just the first order derivative, \[\begin{aligned} \frac{\partial y}{\partial x} = \frac{\partial y}{\partial \alpha} \frac{\partial \alpha}{\partial x} = \frac{\partial y}{\partial \alpha}, \end{aligned}\]

where in the first step we have used the chain rule, and in the second step we have used that \[\frac{\partial \alpha}{\partial x} = \frac{\partial (x - vt)}{\partial x} = 1.\]

Now we can repeat the procedure to obtain the second derivative (i.e. the LHS of the wave equation), \[\frac{\partial^2 y}{\partial x^2} = \frac{\partial}{\partial x} \frac{\partial y}{\partial \alpha} = \frac{\partial (\partial y/ \partial \alpha)}{\partial \alpha} \frac{\partial \alpha}{\partial x} = \frac{\partial^2 y}{\partial \alpha^2},\]

where again we used the chain rule and then that \(\partial \alpha / \partial x = 1\).

Now we do the same for the RHS side, \[\begin{aligned} \frac{\partial y}{\partial t} = \frac{\partial y}{\partial \alpha} \frac{\partial \alpha}{\partial t} = -v\frac{\partial y}{\partial \alpha}, \end{aligned}\]

where this time we used \[\frac{\partial \alpha}{\partial t} = \frac{\partial (x - vt)}{\partial t} = -v.\]

The second derivative is then \[\frac{\partial^2 y}{\partial t^2} = \frac{\partial}{\partial t} \bigg( -v \frac{\partial y}{\partial \alpha} \bigg) = (-v) \frac{\partial (\partial y/ \partial \alpha)}{\partial \alpha} \frac{\partial \alpha}{\partial x} = (-v) (-v)\frac{\partial^2 y}{\partial \alpha^2} = v^2\frac{\partial^2 y}{\partial \alpha^2}.\]

We can now see that this does indeed satisfy the wave equation, i.e. \[\frac{\partial^2 y}{\partial x^2} = \frac{1}{v^2} \frac{\partial^2 y}{\partial t^2} \rightarrow \frac{\partial^2 y}{\partial \alpha^2} = \frac{1}{v^2} v^2\frac{\partial^2 y}{\partial \alpha^2}\]

Derivation of the Wave Equation

There is no single derivation for the wave equation as the same equation arises from many different physical systems. The example below is for a stretched string.

Consider an arbitrarily small segment of a stretched string under tension as shown in Figure 2.

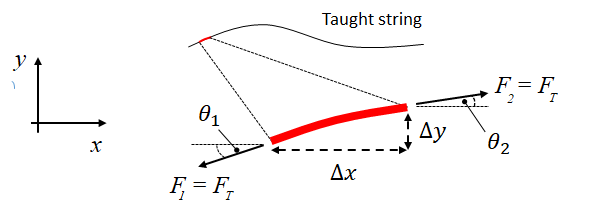
For a string under tension there must be equal and opposite forces acting on each segment along the string. The horizontal forces balance, i.e. \[F_{1,x} = -F_{2,x}\]

and so the total horizontal force, \(F_x = 0\) and we no longer need to consider these.

We are now going to pluck the string so that we are disturbing it entirely in the vertical (\(y\)) direction. The vertical force due to the tension in the string can be written \[F_y = F_{1,y} + F_{2,y} = F_T\sin \theta_1 - F_T \sin \theta_2\]

where \(F_T\) is the tension in the string. It is difficult to work with \(\sin \theta\) because this is a ratio over the hypotenuse which is the length of the segment. However, if \(\theta \ll 1\) we can approximate that \(\sin \theta \approx \tan \theta\). This is more useful because \(\tan \theta\) is the ratio \(\Delta x / \Delta y\). We will write \(S = \Delta x / \Delta y\) so that we have the total vertical force \[F_y = F_{1,y} + F_{2,y} \approx F_T\tan \theta_1 - F_T \tan \theta_2 = F_T (S_2 - S_1) = F_T \Delta S.\]

Now we use Newtons law, \(F = ma\), realising that the vertical acceleration can be written \[a_y = \frac{\partial^2y}{\partial t^2}.\] The mass of the segment of string can be written as \(\Delta m \approx \mu \Delta x\), where \(\mu\) is the mass per unit length of the string. Then, considering the vertical force, we have \[\begin{aligned} F_y &= ma_y \\ F_T \Delta S &= \mu \Delta x \frac{\partial^2y}{\partial t^2} \\ F_T \frac{\Delta S}{\Delta x} &= \mu \frac{\partial^2y}{\partial t^2}. \end{aligned}\]

Finally, we take the limit where the segment becomes infinitesimal, i.e. \(\Delta x\to 0\), \[\begin{aligned} \lim_{\Delta x \to 0} F_T \frac{\Delta S}{\Delta x} &= \mu \frac{\partial^2y}{\partial t^2} \\ F_T \frac{\partial}{\partial x} \frac {\partial y}{\partial x} &= \mu \frac{\partial^2y}{\partial t^2} \\ \frac {\partial^2 y}{\partial x^2} &= \frac{\mu}{F_T} \frac{\partial^2y}{\partial t^2}. \end{aligned}\] We have therefore obtained a wave equation. This immediately tells us that plucking the string will generate a wave which moves along the string. We can read off of the speed of the wave by comparing with the general wave equation, and seeing that \[\begin{aligned} \frac{1}{v^2} = \frac{\mu}{F_T} \\ v = \sqrt{\frac{F_T}{\mu}}. \end{aligned}\]

Harmonic Waves

To understand a system we then want to find solutions to the wave equation that gives displacement \(y\) as a function of position, \(x\), and time, \(t\). There are a large number of solutions, but one of the most general useful ways to write solutions is as an harmonic wave, where each point on the string oscillates with simple harmonic motion.

We could also write \(y = A \sin(kx - \omega t + \delta)\), the only difference being that we need to adjust \(\delta\) by adding \(\pi / 2\) to get the wave to be exactly the same place on the x-axis. It is perfectly acceptable to use either.

We have introduced four quantities by which the harmonic wave solution is parameterised: \(A\), \(k\), \(\omega\) and \(\delta\)

• \(A\) is simply the amplitude of the wave.

• \(k\) is called the wavenumber, it controls how quickly the wave oscillates along the spatial direction.

• \(\omega\) is called the angular frequency, it controls how quickly the wave oscillates in time.

• \(\delta\) is called the phase offset, this controls the starting point of the wave (i.e. the wave when \(x= t=0\)).

As an exercise you can check that this is indeed a solution. Notice that harmonic waves are periodic waves - i.e. they repeat after some interval.

The argument of the cosine/sine, i.e. everything inside the brackets, the \((kx - \omega t + \delta)\), is called the phase. You may sometimes see waves written in the phasor form, \[y = \Re{\exp(i[kx - \omega t + \delta])},\]

where \(\Re\) means to take the real part of a complex number. If you remember Euler’s identity, \[\exp(ix) = \cos(x) + i\sin(x),\]

then you will see that these are the same thing, i.e. \(\Re{\exp(ix)} = \cos(x)\).

Aside: Quite often this written without the \(\Re\), i.e. \(y = \exp(ix)\). This doesn’t mean the wave is complex, you need to remember to take the real part at the end of any calculations you do. The reason we do this is that it’s mathematically simpler to work with exponential than sines - you don’t have to remember all the trig identifies. We won’t use the phasor representation in this part of the course, but it will come up later in your studies.

Visualising Haromonic Waves

To visualise harmonic waves it is convenient to fix one of the variables, \(x\), or \(t\). If we fix \(x\) then we are looking at a single point in time, if we fix \(t\) then we are looking at all the points at a fixed time.

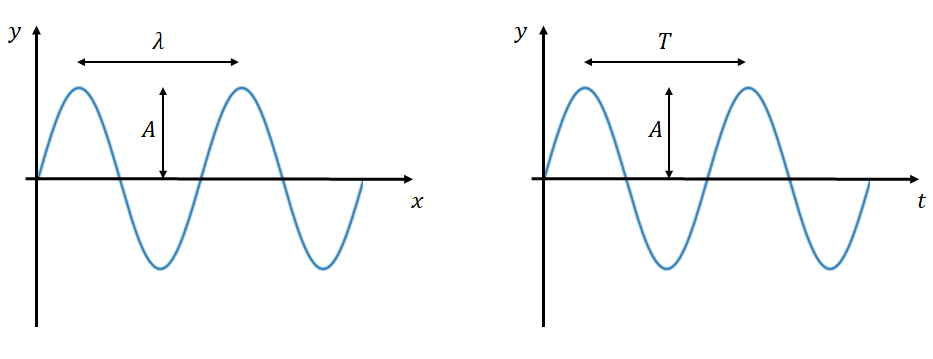
We define the wavelength, \(\lambda\), of the wave as the distance between to identical points (e.g. two peaks) when we have frozen the time variable. This is related to the wavenumber, \(k\), by \[\lambda = \frac{2\pi}{k}.\]

Similarly, the period, \(T\), is the time difference between two peaks when we are looking at a single spatial position, and is related to the angular frequency, \(\omega\), by \[T = \frac{2\pi}{\omega}.\]

Speed of Harmonic Waves

By substituting the expression for an harmonic wave into the wave equation, we can read off that \(v = \omega / k\), or equivalently, \(v = f\lambda\). Another way to see this is to consider a point on the wave moving at speed \(v = \partial x / \partial t\). Since we are considering a fixed point, the phase, \(\phi\), does not change with time, i.e., \[\begin{aligned} \frac{\partial \phi}{\partial t} &= 0 \\ \frac{\partial (kx - \omega t)} {\partial t} & = 0 \\ k\frac{\partial x}{\partial t} - \omega & = 0 \\ v = \frac{\omega}{k} \end{aligned}\]

Doppler Effect

The Doppler effect is the change in frequency of a wave when the source and or receiver are moving relative to each other. The origin and derivation of this is covered in the Special Relativity notes from PHYS3210. The Doppler effect is described by the following equation:

Note that the speeds are defined relative to the medium that the wave is travelling in. So, for example, if we are dealing with sound then this is usually going to be the air. The equation is only valid when the speeds of the objects are much less than the speed of the wave, i.e. \(v_r, v_s \ll v\).

(Note that the Doppler equation is different for light due to relativistic effects, this was covered in PHYS3210 and will not be examined in PHYS3220).

Linearity of the Wave Equation

The wave equation is linear, i.e. it has no powers of \(x\), \(y\), or \(t\) higher than 1. A consequence of this is that if we have two solutions to the wave equation, \(\phi_1\) and \(\phi_2\), then we can make a third solution by adding these together, \(\phi_3 = \phi_1 + \phi_2\).

Aside: Later in your studies you will encounter Fourier theory which says that any function can be written as a sum of sin and cosine terms. This means that any arbitrary wave can be written as a sum of harmonic waves.

Wave Intensity

Imagine a source of waves, emitting in all direction. We can imagine the leading edge of the wave expanding out from the source as a sphere of increasing radius. At an instant in time, the power emitted by the source is therefore distributed over the surface of the sphere. We define the intensity, \(I\), as power, \(P\), over area, \(A\).

Diffraction, Interference and Standing Waves

In this section we will briefly introduce ideas of reflection and interference, topics which you will study in much more detail later on. We will then look at how they combine to leads to the phenomena of standing waves. Finally we will briefly introduce diffraction.

Superposition and Interference

When two waves meet in space, we say they are ‘superimposed’. The resulting disturbance is simply the sum of the disturbance caused by the two waves. This is known as superposition. This linearity make the analysis of waves relatively straightforward. It is a consequence of the the linearity of the wave equation, i.e. there are no powers of \(x\) greater than 1. Not all waves work in this way, for example oceans surface waves are non-linear (leading to all kinds of interesting effects), and in certain media light waves or not linear (giving rise to the field of non-linear optics).

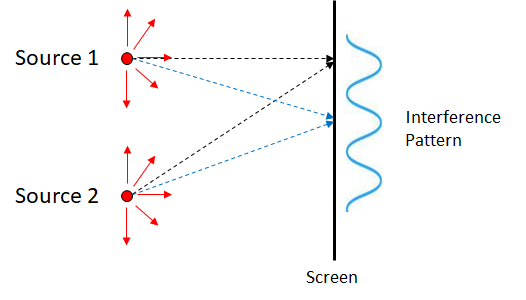
We refer to superposition as interference when the superposition results in a patterns of high and low intensity, e.g. bright and dark for light, loud and quiet for sound. (There is no clear physical difference between superposition and interference, it is more a matter of terminology). Interference can be observed most easily by super-imposing two harmonic waves of the same wavelength and frequency. We also use the terms constructive and destructive interference to refer to when the interference results in a larger or smaller amplitude, respectively.

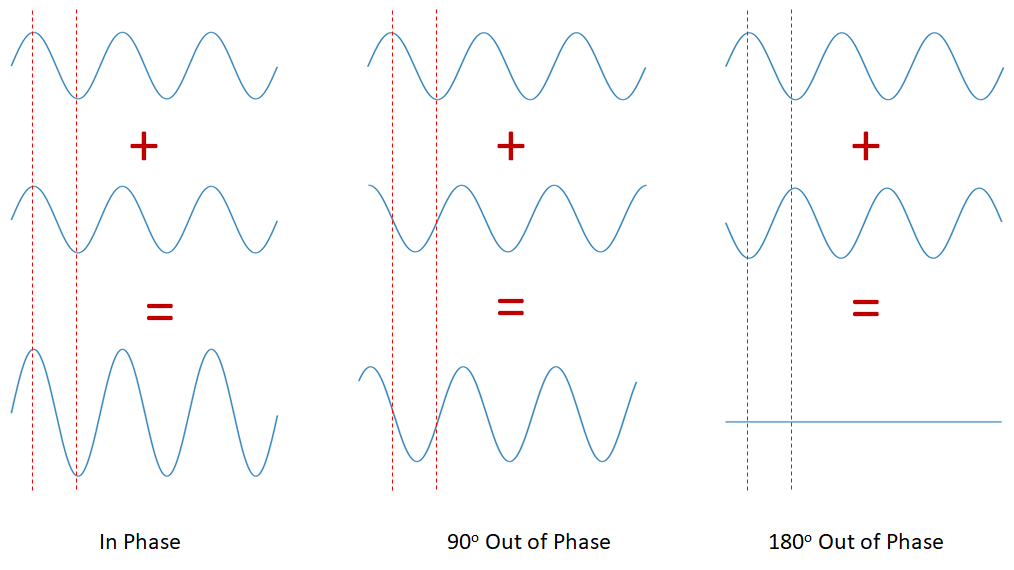
In order to see an interference pattern between two waves of the same frequency, we need some variation in the path length, and hence the phase, so that we alternate between constructive and destructive interference. A simple way to obtain this is to have two point sources, as show in Figure 11.2. At each point along the screen the difference between the two path lengths from the two points sources is different, i.e. there is a different value of \(x\) in the phasor. We therefore have different phase shifts and hence different degrees of destructive and constructive interference at different points along the screen.

Beats

Beating occurs when we have super-position of two waves with similar, but slightly different, frequencies. The results in a third wave of lower frequency. Qualitatively, it can be explained by considering that that a single point in space, the two waves will gradually shift in and out of phase, and so between constructive and destructive interference. This creates a low frequency wave, with the beat frequency given simply by the different in frequencies.

A full derivation of the beat frequency is provided in Tipler Section 16-1.

We can therefore us the beat frequency to determine, trivially, the difference in frequency between to the two waves. This is one way to tune an instrument using a tuning fork. We play a note and then ring the tuning fork. The instrument is then tuned by adjusting until the beat frequency becomes very small.

Coherence - Non-examinable

We might wonder why we don’t see interference patterns everywhere, after all light is wave so why don’t we see interference between two light from two different light bulbs? The answer lies in a concept called ‘coherence’. Light from a light bulb can be though of as being made up of many different waves, each with a different phase. The phase of each waves also varies randomly over time. This makes a light bulb an ‘incoherent source’. We don’t see interference patterns patterns because the interference pattern changes so rapidly in space and time that it is averaged out to a uniform intensity. An example of a coherent source is a laser - and we can create interference using a laser beam. It’s also possible to make partially coherent light from incoherent light by passing it through a very small pinhole. This is how interference experiments (such as Young’s slit experiment or the Michelson-Morley experiment) were able to be conducted long before lasers were invented. You will learn much more about interference conditions and coherence later in your studies.

Reflection and transmission of waves

When a wave strikes a boundary between two regions where the wave would travel at difference speeds, some portion of the wave is reflected. The returning wave is inverted if the second medium has a lower wave speed. For sounds waves in air, different speeds are caused by different densities (e.g. sounds travels faster in solids than in air). We could also imaging a light string attached to a heavier string. Since a wave on a string has a lower speed in a heavier string, a wave on the light string would be partially reflected and inverted at the boundary.

If we were to take a single string and fix it at one end, we can consider this as being like a wave passing onto a more massive string, in the limit that the speed in the second string becomes zero. And so we have, \[r = \frac{v_2 - v_1}{v_2 + v_1} = \frac{0 - v_1}{0 + v_1} = -1,\] meaning that the whole of the wave is reflected with an inversion.

The fraction of the wave transmitted is simply \(t = 1-r\), \[t = 1- \frac{v_2 - v_1}{v_2 + v_1} = \frac{v_2 + v_1 + v_2 - v_1}{v_2 + v_1} = \frac{2v_2}{v_2 + v_1}.\]

Notice that we always have \(t > 1\), i.e. the transmitted wave is never inverted.

Standing Waves

A standing wave is created when we confine a wave in such a way that it interferes with its own reflection. For example, if we anchor a string at either end, a wave travelling along the string will reflect from the anchor point and return back along the string. In certain circumstances, the interference results in a fixed pattern, known as a standing wave. This requires that the frequency of the wave is one of several ‘modes’ of the particular system we have. These frequencies are called the resonant frequencies and the accompanying wavefunction is called a mode of vibration. The lowest resonant frequency is called the fundamental frequency and the higher resonant frequencies are called overtones.

Some example of standing waves on a string are shown in the figure below. We can identify points at which the amplitude is always zero - these are called nodes, labelled N in the figure. The points mid-way between the nodes, where the amplitude is at a maximum, are called anti-nodes, labelled AN.

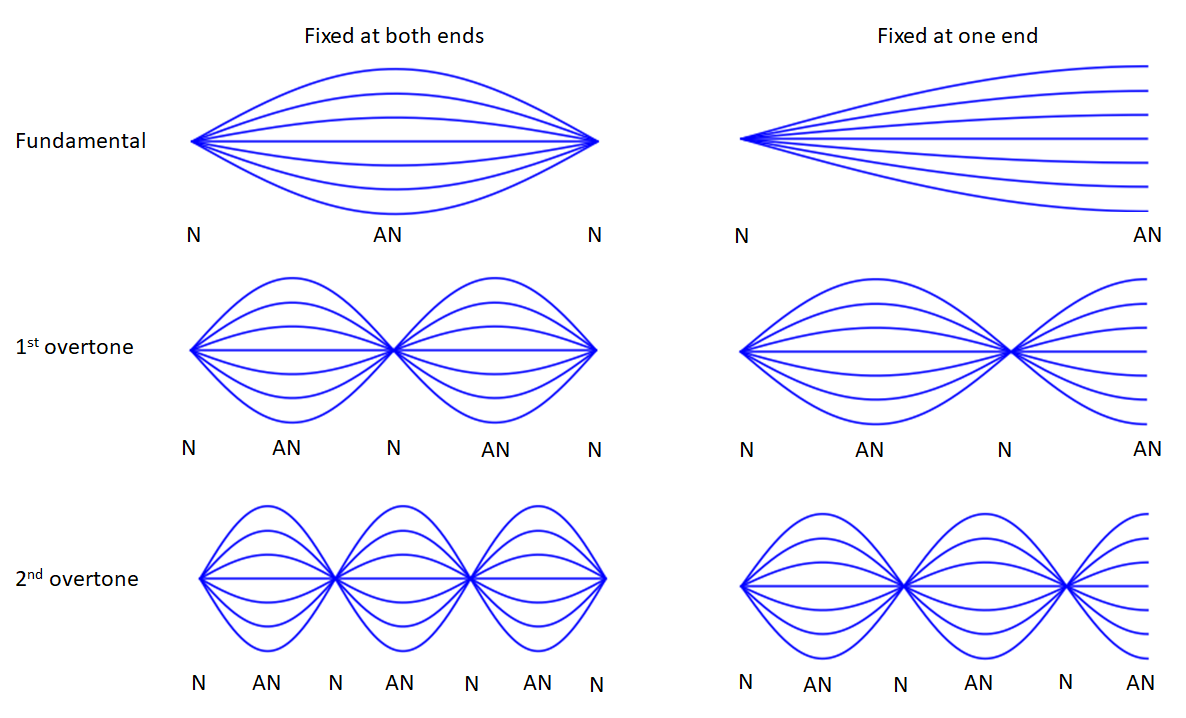
We can predict the harmonic frequencies from the speed of the wave and the length of the string. First consider a vibrating string of length \(L\) where both ends are fixed (such as a guitar string). It must be that each end of the string is a node (i.e. amplitude is zero at all times). The lowest frequency of harmonic wave satisfying this would be the case where there is one half-wave along the full-length of the string, i.e., \[\lambda = 2L.\] The next lowest frequency would have \(\lambda = L\), then \(\lambda = 2L/3\) and so on. In general, \[\lambda_n = \frac{2L}{n},\]

where \(n\) is a positive integer. Using \(f = v / \lambda\), the resonant frequencies are therefore \[f_n = n\frac{v}{2n}.\]

For the case where one end of the string is free, then we have a node at one end and an anti-node at the other. We therefore require wavelengths of \(\lambda = L/ 4\), \(\lambda = 3L / 4\) and so on. The resonant frequencies therefore occur at \[f_n = n\frac{v}{4L}.\] for odd values of \(n\), i.e. \(n = 1,3,5...\)

Diffraction

Diffraction is a phenomenon that occurs when a wave is partially blocked by an obstacle. It is a phenomenon that is unique to waves, distinguishing them from classical particles. It is a consequence of interference, but the details are covered in later modules. It can loosely be described as ‘bending’ of the wave which occurs near the edge of the obstruction. By ‘near’ we mean within a few wavelengths. When waves pass through gaps that are similar in size to their wavelength, essentially all of the wavefront is close to the edge, and the diffraction effects are very obvious. However, for gaps which are much larger than the wavelength, diffraction effects are small. Sound has wavelengths of metres, and so sounds readily diffracts around everyday objects. It is diffraction as well as reflection, which allows us to hear around corner. In contrast light has a wavelength of around 0.5 micrometers and so diffraction effects are not easily observed - the geometrical approximation that light travels in straight lines is generally a good ones.