Physics and Astronomy, University of Kent
In this final section, we move to looking at wave phenomena in electric and magnetic fields, otherwise known as electromagnetic radiation or light. A full description of the propagation of light is a complex endeavour, understanding it rigorously involves solving Maxwell’s Equations. Here, we will look at some of the underlying concepts of electromagnetic waves, relating to the physics of waves you studied earlier in the module. We will also introduce the idea of polarisation of light. Combined with the geometric optics studies in PHYS3040, this will complete your introductory optics, which will be built on later in PHYS6040.
Light is a wave in the electromagnetic field (and so you should make sure you are happy with the waves section of the module before continuing). Later in your degree you will derive the wave equation from Maxwell’s equations, but for now we will just begin with the wave equation for the electric field in a vacuum. \[\frac{\partial^2 E(x,y,z,t)}{\partial x^2} + \frac{\partial^2 E(x,y,z,t)}{\partial y^2} + \frac{\partial^2 E(x,y,z,t)}{\partial z^2} - \frac{1}{c^2} \frac{\partial^2 E(x,y,z,t)}{\partial t^2} = 0.\] We can write a similar equation for the magnetic field, but it turns out that the solutions are essentially the same, so by convention we only work with the electric field. Although you may not have studied vector calculus yet, and so we will not use it here, you will often see this written more compactly as \[\nabla^2 E - \frac{1}{c^2} \frac{\partial^2 E}{\partial t^2} = 0.\] The two equations mean the same thing (at least in Cartesian co-ordinates), \(\nabla^2\) is a shorthand for taking the sum of the 2nd order partial derivatives with respect to \(x\), \(y\) and \(z\). Notice that we have written \(E\) and not \(\vec{E}\), i.e. we are treating the field as a scalar and not a vector. For this reason, the equation is sometimes called the scalar wave equation. A full treatment would need to use the vector form of \(E\) which makes things a lot more complicated and requires maths you may not have seen yet.
However, we can cheat a little and only worry about the direction the wave is travelling in, and align our co-ordinate system so that we call this the z-axis. Then, working in 1D we have the simpler and more familiar wave equation \[\frac{\partial^2 E(z,t)}{\partial z^2} - \frac{1}{c^2} \frac{\partial^2 E(z,t)}{\partial t^2} = 0.\] Now, it turns out that there are quite a lot of solutions to this equation (and remember that any linear combinations of solutions will also be solutions). A useful way to write the solutions is as harmonic waves, \[E(z) = A \sin(kz - \omega t + \theta).\]
Depending on how far you have progressed with studying differential equations this may or may not be obvious to you, but we can check it is a solution by substituting it back into the left hand side of the 1D wave equation.
\[\begin{aligned} \frac{\partial^2 E(z,t)}{\partial z^2} - \frac{1}{c^2} \frac{\partial^2 E(z,t)}{\partial t^2} &= \frac{\partial^2 \left( A \sin(kz - \omega t + \theta) \right)}{\partial z^2} - \frac{1}{c^2} \frac{\partial^2 \left( A \sin(kz - \omega t + \theta) \right)}{\partial t^2} \\ &= Ak^2\sin(kz - \omega t + \theta) - \frac{1}{c^2} A\omega^2 \sin(kz- \omega t + \theta) \\ &= k^2 - \frac{\omega^2}{c^2} \end{aligned}\] There is no no \(z\) or \(t\) dependence, so this is a solution. Setting equal to 0, as in the wave equation gives, \[c=\omega / k.\]
Since any linear combination of solutions is also a solution, we can make all kinds of interesting solutions by taking sums of large numbers of our sine-wave solutions with different values of \(k\), \(\omega\), and \(\theta\). If we take an infinite number of solutions we can even make a square-shaped wave! When you later study Fourier transforms this will become more apparent, so we won’t dwell on it for now.
Instead, let’s look at what the terms in the solution mean in more detail. Like any wave, a light wave can be described in terms of its amplitude (\(A\)), frequency (\(f\)), wavelength (\(\lambda\)), period (\(T\)), and initial phase (\(\theta\)). We also define the wavenumber, \(k = 2\pi/ \lambda\) and the angular frequency \(\omega = 2\pi f\), with \(f = 1/T\). Note that since we have shown \(c=\omega /k\) we immediately then get \(c = f \lambda\).
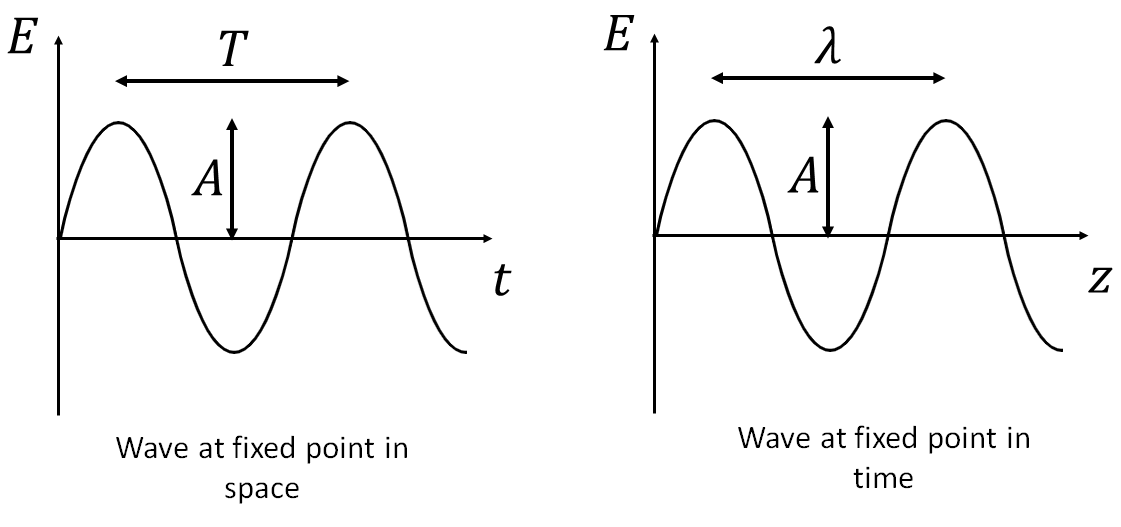
From the solution for \(E\) it is clear that the field varies in both time and space, so when we draw a wave we need to be clear what we are drawing - either the spatial wave at a fixed point in time (\(t\)), or the temporal wave at a fixed point in space (\(z\)) (see Figure 1).

The argument of the \(\sin\) function is called the phase, \(\phi\) where \[\phi = kx - \omega t + \theta,\] and so \[E = A \sin(\phi).\]
This phase tells us the point in the wave cycle we have reached at particular point in space and time. This is expressed as an angle, with a phase of \(2\pi\) equivalent to a complete cycle of the wave. After a phase of \(2\pi\) we are back where we started, so for example a phase of \(5\pi/2\) is the same as a phase of \(\pi/2\). Don’t confuse the total phase (which is everything inside the sine) with the initial phase, \(\theta\) which is an offset to the phase.
Notice that we can write \[k = \frac{\partial \phi}{\partial z},\] and, \[\omega = -\frac{\partial \phi}{\partial t} ,\] which makes it explicit that wavenumber \(k\) tells us how the phase changes with position, and the angular frequency \(\omega\) tells us how the phase changes with time.
You will have come across refractive index already in the context of geometrical optics, but now we can think about it in the context of the wave theory of light. The velocity of light depends on the medium it is travelling through. It can never exceed the speed of light in a vacuum, \(c\), that is to say it propagates more slowly in other materials. The refractive index, \(n\), of that medium determines the velocity.
The refractive index, \(n\), of a medium is the inverse of the ratio of the speed of light in that medium, \(v\), to the speed of light in a vacuum, \(c\): \[n=c/v\]
By definition, the refractive index of a vacuum is 1. Air is about 1.003, which we often take to be 1 for practical purposes. Water has a refractive index of 1.4, and glass varies from 1.4-1.7.
From the solution to the wave equation in free space, we saw that \[v = c = \frac{\omega}{k},\]
or equivalently \[v = c = f\lambda,\] which you can verify from \(\omega = 2\pi f\) and \(k = 2\pi/\lambda\). When light enters a medium with \(n > 1\), then \(v < c\). In which case either \(f\) or \(\lambda\) must change. In fact it is the wavelength, \(\lambda\), which changes with \(n\), so that \[\lambda_{medium} = n\lambda.\] The frequency and angular frequency, \(f\) or \(\omega\), are fixed, and do not depend on the refractive index of the medium.
For most materials, \(n\) decreases slightly with wavelength over the visible region. This gives rise to an effect known as dispersion. Since different wavelengths of light will travel at different speeds in the material, a short pulse of multi-wavelength light will become spread out. This is the ultimate limit on how much data can be sent over fibre optics. It also explains how a spectrum is produced from a prism.
Earlier in the module you will have discussed the difference between phase velocity and group velocity. The velocity we are referring to above is the phase velocity of light, and the refractive index, \(n\), tells us what happens to the phase velocity.
If we have light of a single wavelength, then the phase velocity and the group velocity are the same. But if we have light made up of multiple wavelengths, then each wavelength will see a different refractive index and so have a different phase velocity. The group velocity is given by \[v_g = \frac{d \omega}{d k}.\] In a non-dispersive material, i.e. where the refractive index is constant with wavelength, then from \(v = \omega/k\) we can easily see that \[\frac{d \omega}{d k} = v\] which is known as linear dispersion. A particular example is a vacuum, in which case \(v = c\).
More generally through, when \(n\) depends on \(k\), then \(v_g \ne v\). A pulse of light, which for reasons you will study more deeply later in your degree must be made up of more than one wavelength of light, therefore has different group and phase velocities, i.e. the pulse travels at a different speed. In some special circumstances it is possible to have \(v > c\), but we always have that \(v_g <c\). Information travels at the group velocity, not the phase velocity, and so this is consistent with the theory of special relativity.
It is often helpful to talk about the wavefront of a wave. A wavefront is a surface of constant phase. The shape of the wavefront can tell us how the light is propagating. For example, a planar wavefront describes a collimated beam of light (i.e. plane waves). A spherical wavefront describes light which is converging from - or diverging to - a point.
If we have a point source, then the wavefront at a time \(t\) is at a distance \(r\) from the point, where \(r(t) = c t\). Here, \(c\) is the speed of light in a vacuum. If we working inside a material then we will need to modify this, as described below.
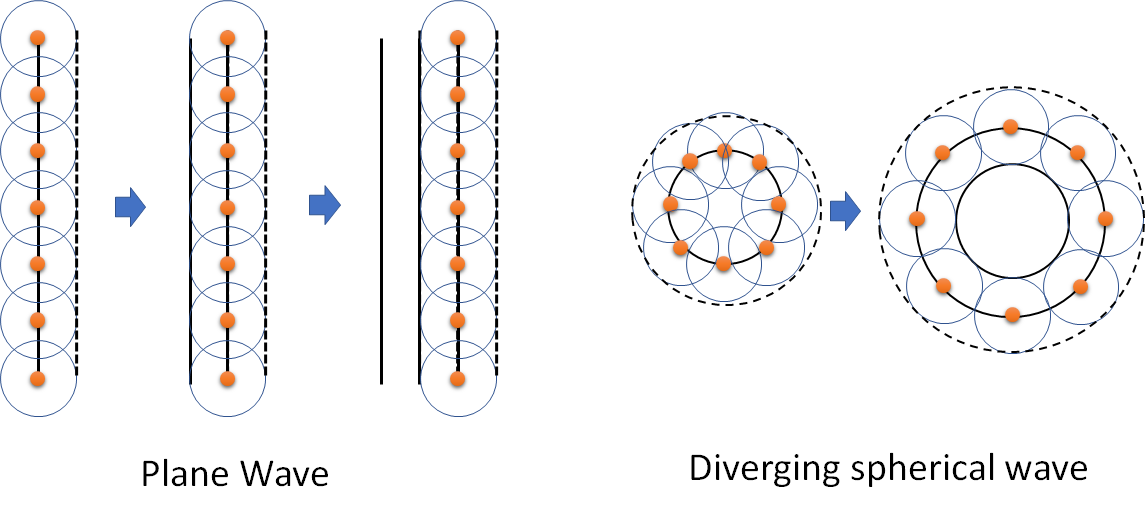
Huygen’s principle provides a simple rule to predict the propagation of a wavefront of light. It is empirical, in the sense that is was derived by observations rather than than from any fundamental considerations.
Each point on a wavefront acts as source of secondary wavelets. These wavelets have the same velocity and frequency as the original wave. The envelope of these wavelets forms the new wavefront.
This says that if we have a wavefront, we can calculate how the wavefront at some future point in time will look by assuming that each point on the wavefront acts as a source of spherical waves. We then take the envelope of these new waves, and that is now the new wave.
Non-examinable Aside: Huygen had no explanation of why this seemed to be true. In fact the reason can only be understood in terms of a travelling wave solution to Maxwell’s equations, and in particular the approximate description of this given by scalar diffraction theory, which you will be introduced to in PHYS6040.
The flaw with Huygen’s principle is that it also suggests that there is a wave running backwards, i.e. there is nothing to encode the direction of the wave. This problem was later solved by Kirchhoff, but that is beyond the scope of this course. Suffice it to say that destructive interference results in the ‘backwards’ wave having zero intensity.
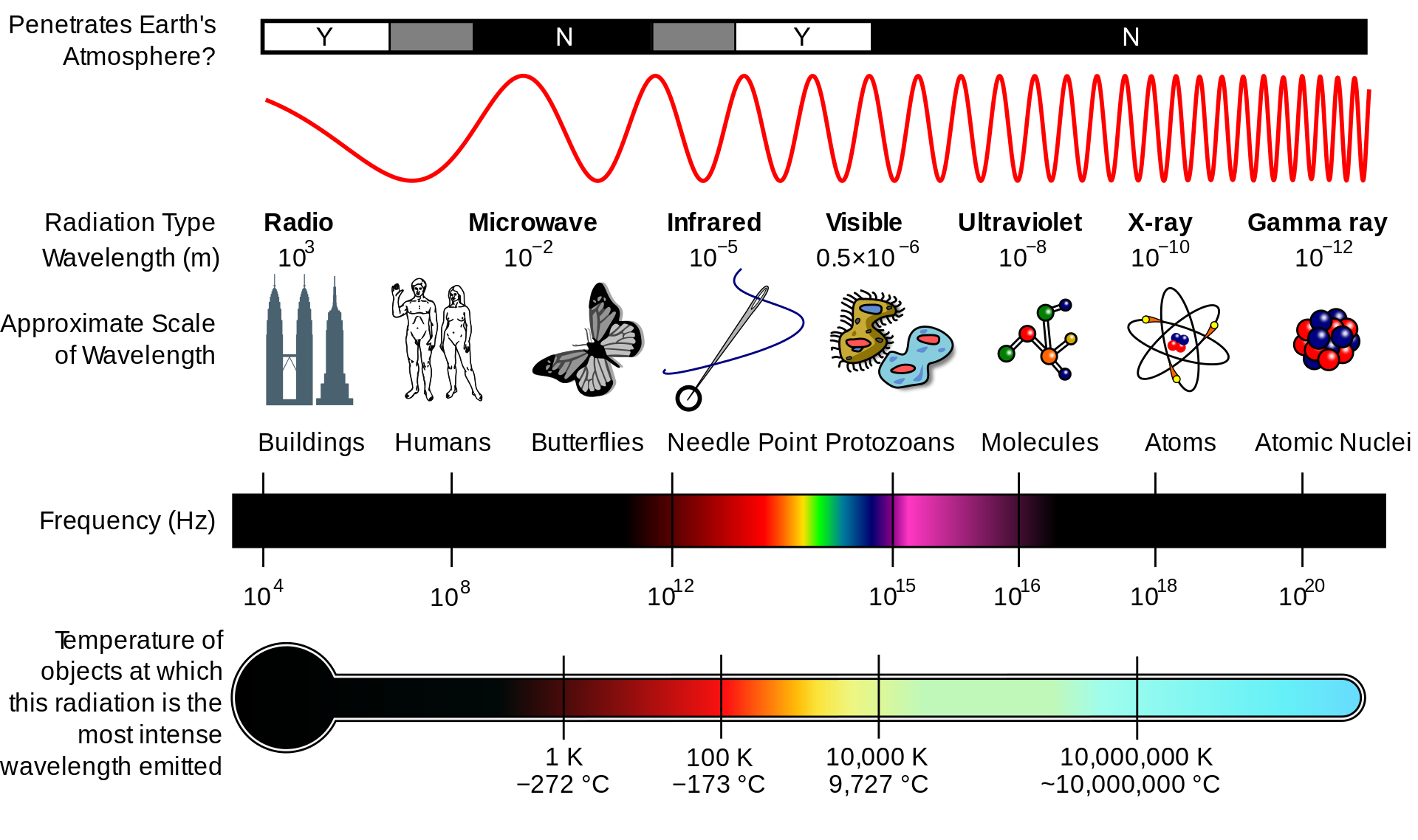
The frequency of electromagnetic radiation, or light, leads to radically different interactions with the material world. The electromagnetic spectrum is illustrated in Figure 3 below as a function of frequency (or wavelength in a vacuum). We encounter electromagnetic waves with frequencies spanning over 16 orders of magnitude:
Gamma rays (\(f > 10^{19}\) Hz) are produced in nuclear and particle physics processes. They are highly penetrating and cause damage to biological tissue at moderate levels. They also have a number of applications in medical imaging (PET, SPECT cameras) and medical radiotherapy (such as Iodine therapy).
X-rays (\(10^{16}~\mathrm{Hz} < f < 10^{20}~\mathrm{Hz}\)) overlap gamma rays in terms of frequency, but are generally distinguished by the method of production - x-rays are emitted from outside the nucleus, such as electrons in orbitals or rapid deceleration of atom. Again they are highly penetrating but easier to produce and work with than gamma rays, and so they are widely used in medical and industrial imaging
Ultraviolet rays (\(7.5\times10^{14}~\mathrm{Hz} < f < 4\times10^{16}~\mathrm{Hz}\)) are present in sunlight and, while non-ionising, can cause damaging to living tissue. Exposure of human skin is associated with an increased risk of skin cancer, while short-wavelength UV light can be used to sterilise surfaces. Longer wavelength UV light can be used to excite fluorescence in some molecules.
Visible light (\(4.3\times10^{14}~\mathrm{Hz} < f < 7.5\times10^{14}~\mathrm{Hz}\)), while a small part of the spectrum, is the most obvious form of EM radiation and the only part of the spectrum directly detectable by the eye. Blue light is at the shorter wavelength end, red light is at the longer wavelength end.
Infrared Light (\(3\times10^{11}~\mathrm{Hz} < f < 4.3\times10^{14}~\mathrm{Hz}\)) is emitted by a black body near room temperature, and so has applications in thermal imaging. It has many other applications such as in astronomy and communications (e.g. your TV remote control).
Microwaves (\(3\times10^{9}~\mathrm{Hz} < f < 3\times10^{11}~\mathrm{Hz}\)) are widely used in communications and related applications, as well as for cooking in a microwave oven (at 2.45 GHz)
Radio waves (\(3\times10^{3}~\mathrm{Hz} < f < 3\times10^{9}~\mathrm{Hz}\)) are again very widely used for communications, and also feature prominently in astronomy.
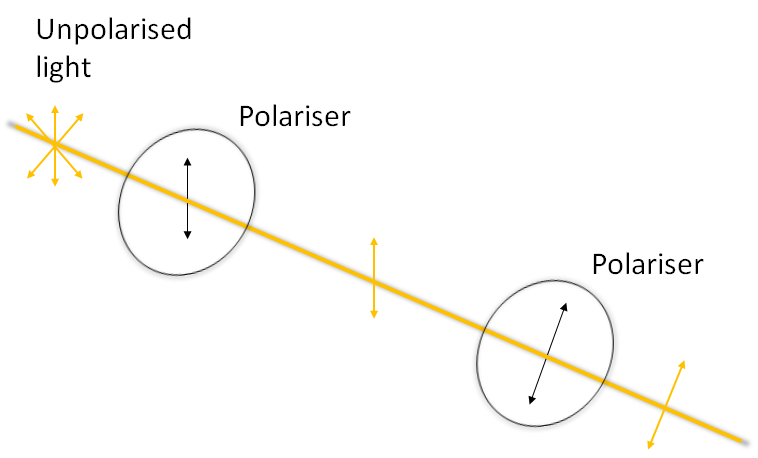
Light is a transverse wave, the electric field (and the magnetic field) is perpendicular to the direction of propagation of the light. In linearly polarised light, the E-field points negative or positive along a single direction. In circularly polarised light, the direction of the electric field rotates as the light propagates. In elliptically polarised light the amplitude of the wave varies as the direction rotates. Unpolarised light is made of up of fields pointing in all directions.
Unpolarised light can be linearly polarised using a polariser such as polarising film. The film has a transmission axis, which is the orientation of polarisaton of light which will be transmitted. If the incident light is unpolarised then the transmitted light will be polarised in the same direction as the transmission axis. The incident light will be attenuated by a factor of 2, i.e. half the intensity is lost.
However, if the incident light is already linearly polarised before it hits the polariser then the fraction of light which will be transmitted is given by Malus’ Law:
\[\frac{I_{transmitted}}{I_{incident}} = \cos^2 \theta\] where \(\theta\) is the angle between the incident polarisation direction and the transmission axis. If two polarisers are placed at 90 degrees to each other, known as ‘crossed polarisers’ then the transmitted intensity is zero.
Note that Malus’s Law doesn’t work for unpolarised light. Unpolarised light will be polarised along the axis of the polariser with a loss of half its intensity.
An interesting consequence of Malus’s Law is illustrated in the following. Consider an initial situation with two polarisers, set up with their axes at \(90^o\) to each other (crossed polarisers). Unpolarised light hits the first polariser and is then linearly polarised along the axis of the polariser. When it strikes the second polariser, we then have \(\theta = 90^o\) and so the transmitted intensity is 0.
Now imagine inserting a third polariser between the initial two. We orient this polariser so that the axis is at \(45^o\) to the first polariser (and so also at \(45^o\) to the second).
The angle between the light polarised by the first polariser, with intensity (\(I_1\)) and the axis of the second polariser is \(45^o\) and so: \[I_2 = I_1 \cos^2(\theta) = I_1\cos^2(45^o) = 0.5I_1\] Now, when this light hits the final polariser, again we have \(\theta = 45^o\), \[I_3 = I_2 \cos^2(\theta) = I_2\cos^2(45^o) = 0.5I_2 = 0.25I_1\] So by inserting an additional polariser we have increased the amount of light making it through the system!
These kind of effects are strongly associated with wave phenomena, and are require more elaborate explanations if we try to explain light as a stream of classical particles. But what is even more interesting is that we get the same result even if we work with individual photons, at which point we are straying into quantum mechanics (and quantum optics), which will have to wait for now!