Physics and Astronomy, University of Kent
Magnetic field are the second part of the electromagnetic field. In later courses you will understand more about the origin of the magnetic field, and how it is related to the electric field, but in PH322 we will restrict ourselves to a description of how charged particles behave in magnetic fields, and some applications of this.
If we have a magnetic flux density, \(\vec{B}\), then a charge \(q\) moving at velocity \(\vec{v}\) in that field experiences a force, \(\vec{F}\) given by:
\[\vec{F} = q\vec{v}\times\vec{B}\]
This defines the unit of magnetic field, the Tesla (T). Note that the magnetic flux density is sometimes known informally as the magnetic field strength, although strictly this is \(H = B/\mu_0\), where \(\mu_0\) is the permeability of free space, \(4 \pi \times 10^{-7}\).
\[1 \mathrm{ T = 1 \frac{N/C}{m/s} = 1 \frac{N}{Am}}.\]
In practice we rarely experience fields anywhere near 1 T; the magnetic field from the Earth is around \(10^{-4}\) T, an amount which is also known as 1 Gauss (G). The magnets in modern Magnetic Resonance Imaging (MRI) systems can reach a few Tesla, and require strict protections to prevent magnetic materials entering the controlled area and being pulled in the magnet.
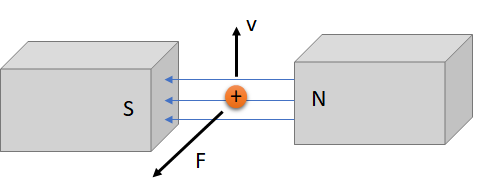
Note that the force is the cross product of the velocity and the field. So it is perpendicular to both, i.e. \(\vec{F}.\vec{B} = 0\). A convenient way to remember the direction in which the force points on a positive charge is the Right Hand Rule, shown in Figure 1. Curl your fingers as if rotating the velocity vector into the magnetic field vector. Your thumb then points in the direction of the force.

See Tipler/Mosca Example 26-1.
Recall that the work done by a force is \[W=\int F. d\vec{r}\] where \(d \vec{r}\) is the vector describing the motion of the particle. But the magnetic force is always perpendicular to the motion of the particle, i.e. \(\vec{F}.\vec{dr} = 0\). So the magnetic force does no work. This means it cannot change the kinetic energy of a particle. Or, in other words, it changes the direction of the velocity, but not the magnitude.
Magnetic field lines are a similar concept to electric field lines, but with important differences:
While electric field lines have sources and sinks - electric charges - there are no sources or sinks of magnetic field lines. A magnetic has two poles - and these two poles always appear as a pair. If we break a magnet in half, we end up with two magnets, each with two poles. So magnetic field lines always form complete loops. They emerge from the North pole end of the magnet and enter the South pole end (although they don’t emerge or enter a point at the poles).
Magnetic field lines do not point in the direction of the Lorentz force. The Lorentz force is perpendicular to the field lines.
Consider a particle of charge \(q\) and mass \(m\) moving on the x-y plane of a cartesian co-ordinate system i.e. \(\vec{v} = v_x\hat{i} + v_y\hat{j} + 0\hat{k} = (v_x,v_y,0)\). There is a magnetic field pointing in the z direction, i.e. \(\vec{B} = 0\hat{i} + 0\hat{j} + B\hat{k} = (0,0,B)\).
The Lorentz force on the particle is given by: \[\begin{aligned} \vec{F} &= q\vec{v} \times \vec{B} \\ &= q(v_yB\hat{i} - v_xB\hat{j}) \end{aligned}\]
As we expect, there is no \(\hat{k}\) component of the force. From Newton’s Law, a force produces an acceleration, \(\vec{F}=m\vec{a}\). So \[q(v_yB\hat{i} - v_xB\hat{j}) = m(a_x\hat{i} + a_y\hat{j} + a_z\hat{k})\] and so: \[\begin{aligned} a_x &= qBv_y/m\\ a_y &= -qBv_x/m\\ a_z &= 0 \end{aligned}\] You may recognise these as equations of motion which describe circular motion. So the charged particle will follow a circular path on the x-y plane. We can calculate the radius (\(r\)) of this circular motion by making use of the centripetal acceleration equation. Since the magnitude of the velocity will not change (the magnetic field does no work) we can work in terms of the magnitude of the velocity \(v\), and centripetal acceleration \(a=v^2/r\). \[\begin{aligned} a &= \frac{v^2}{r} = \frac{qBv}{m} \\ r &= \frac{mv}{qB} \label{eq:1} \end{aligned}\]
The period, \(T\), is then given by \[\begin{aligned} T &= \frac{2\pi r}{v} \\ T &= \frac{2 \pi (mv/qB)}{v} = \frac{2 \pi m}{qB} \end{aligned}\]
And the frequency, \(f\), by \[\begin{aligned} f &= 1/T \\ f &= \frac{qB}{2 \pi m} \end{aligned}\]
Note that the radius depends on the initial velocity, \(v\), while the period depends only on the magnetic field strength, mass and charge. If there is an initial velocity in the z direction then the particle will follow a helical path.
See Tipler/Mosca Example 26-4.
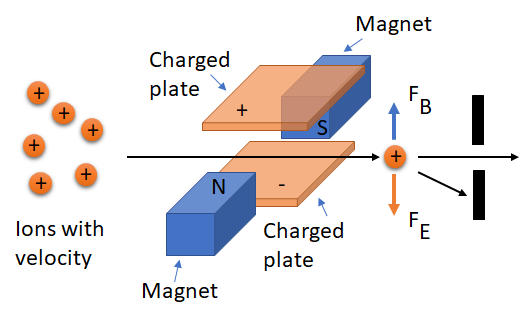
A velocity selector is an instrument which allows charged particles (ions) with a specific velocity to be separated from particles with a different velocity. It is often used with a mass spectrometer, as discussed below.
Opposing electric and magnetic fields are set up in such a way that they exactly balance each other for a specific velocity of the charged particle, as shown in Figure 2. The Coulomb force due to the electric field from the charged plates is given by \(F_E = qE\), and the Lorentz force due to the magnets is given by \(F_B = qvB\). Hence the two forces balance when \(v=E/B\), and so only ions moving at this velocity will be un-deflected and pass through the hole.
The mass spectrometer allows the mass of isotopes to be measured. It exploits the result we derived above, which says that the radius of the circular motion of a charged particle in a magnetic field depends on its mass.
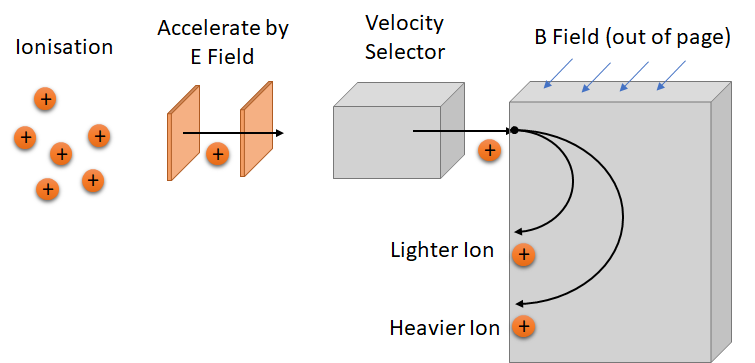
A sample is vapourised and ionised (forming charged particles). The ions are then accelerated by an electric field, across a potential of \(\Delta V\). They therefore lose a potential energy of \(q\Delta V\) and hence gain the same amount of kinetic energy. \[1/2 mv^2 = q\Delta V\]
The ions move into a magnetic field and so experience a Lorentz force, moving in a circular path. Re-arranging the equation for the radius of this path, \(r\), in terms of \(v\) and substituting this in, we obtain \[1/2 m\frac{r^2q^2B^2}{m^2} = q\Delta V\]
We can write this in terms of the mass to charge ratio: \[\frac{m}{q} = \frac{B^2r^2}{2\Delta V}\]
Therefore, by the location where the ion hits the detector, we know the radius of its path and hence its mass-to-charge ratio. If we know the charge on each ion, this allows us to calculate the mass. We can select only ions with a certain charge using a velocity selector (described above), since ions with a different charge will have experienced a different acceleration due to the electric field, and so be moving at a different velocity.
One application of mass spectrometry it to determine the ratios of different isotopes in a material. For example, carbon dating is performed by determining the ratio of Carbon-12 to Carbon-14.
See Tipler/Mosca Example 26-5, 26-6.
A cyclotron is a type of particle accelerator. It can be used to accelerate charged particles to high speed for use in scientific experiments or as radiation sources for medical imaging.
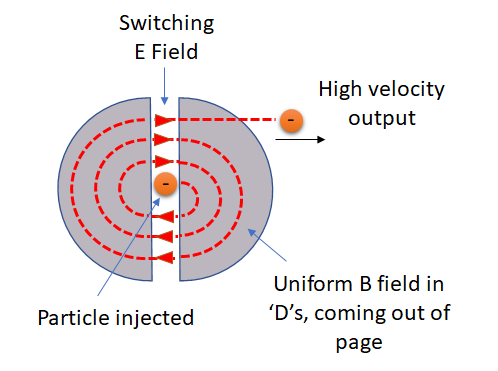
The simplest type of accelerator is a linear accelerator, in which an electric field is used to accelerate a charged particle via the Coulomb force. However, there is limit to the maximum potential difference which can be created before the breakdown voltage of air is exceeded, and this limits the velocities which can be created in a linear accelerator. In a cyclotron, the same electric field is used multiple times.
As shown in Figure 4, charged particles are injected in the middle of the cyclotron, in the gap between the ‘D’s. An electric field accelerates the charged particles, to the right in the case of the diagram. Magnetic fields in the ‘D’s bring the particles in a circular path back to the gap. The electric field is then switched, accelerating the particles again, this time to the left. Again, the B-field causes them to follow a circular path, although this time with a larger radius (due to the larger velocity). This continues, with the particles spiralling out, accelerating each time they cross the gap, until they leave the cyclotron at high speed.
The final velocity and the radius of the outermost loop are linked by Equation [eq:1]. \[r_{max} = \frac{mv}{qB} \implies v = \frac{qBr_{max}}{m}\] And so the maximum possible velocity depends on both the strength of the B-field and the size of the ‘D’s, but not on the accelerating potential difference.
See Tipler/Mosca Example 26-7.