A conductor is a material in which charge is free to move. An insulator is a material where charge is fixed in place. The most common conductors are objects made from metal, although other conductors include electrolytes, plasmas and graphite. Semi-conductors lie somewhere in between, and are useful because the conductivity can be altered.

Charging by Induction

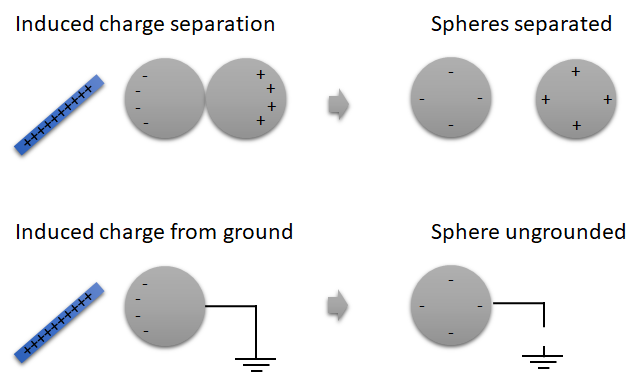
Charging by induction is a way of charging a conductor. Consider two metals spheres, which are touching, as shown in Figure 1. A positively charged rod is brought close to one of the spheres, causing negative charge to flow to that sphere and a positive charge to appear on the other sphere. The spheres are then separated, and even after the rod is withdrawn, the two sphere now retain their charge.

A similar effect can be had with one sphere which is connected to ground. For our purposes we can think of ground as being an infinite source of free charge. We now bring a positively charged rod close to the sphere, causing free negative charge from ground to flow into the sphere. If we break the ground connection, and take away the rod, we now have a negatively charged sphere.

Electric Field Inside a Conductor

If an electric field exists inside a conductor, the free charges will feel an electric force. They will then move until the electric field is zero. So the charges inside the conductor create a field which cancel the external electric field. Hence, over any practical timescale, the conductor is in static equilibrium, and the net charge inside the conductor is zero.

Any excess free charge within a conductor is found to lie at the edge of the conductor. This has to be the case, because otherwise there would be field lines coming out of charges somewhere inside the conductor, and so the electric field wouldn’t be zero.

Field and Potential of a Charged Conducting Sphere

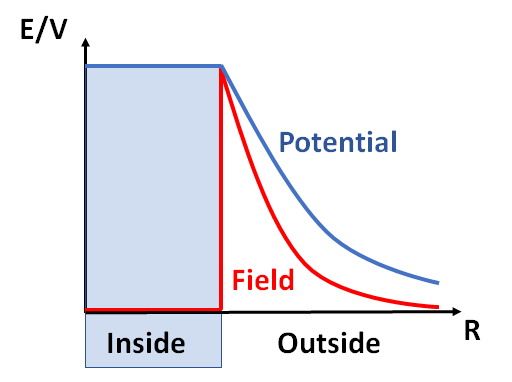
Inside a conducting sphere the electric field is zero everywhere.

Far away from sphere, the sphere is going to look like a point charge. So, we expect the electric field to go as: \[E = \frac{Q}{4\pi\epsilon_0r^2} \label{fieldsphere}\]

where \(Q\) is the total charge of the sphere.

Now, the question is, what happens outside of the sphere, close to the sphere? The answer is that equation [fieldsphere] holds there as well. You will see an elegant proof for this in Stage 2 when you study Gauss’ Law, but for now this is given without proof.

For potential, this means that, outside the sphere, the potential is, as for a point charge, \[V = \frac{Q}{4\pi\epsilon_0r} \label{fieldpot}\]

Finally, for the potential inside the sphere, we have to be careful. It is not zero, because the potential is the integral of the field along a line from infinity. So, the electric potential increases (or decreases for negative \(Q\)) from infinity up to the edge of the sphere, and then it is constant inside.

This is summarised in Figure 2.