Physics and Astronomy, University of Kent
Now that we have defined the electric field it once again seems we should be finished. However, it is useful to define something called the electric potential. Note that the electric potential is not the same thing as electric potential energy, although the two are closely related. We will discuss electric potential energy first.
Consider a positive charge, \(q\) which is generating an electric field. We have another positive charge, which we call the test charge, \(q_0\), which is very far away. We now bring the test charge towards \(q\).
The two charges will repel each other, so this requires effort and we have to do work. The electrical potential energy therefore increases, just like how the gravitational potential energy increases if we push something up a hill. If we let go of the charges, they will fly apart, and this electric potential energy becomes kinetic energy, and the electrostatic force is doing work. Of course, the total energy is always conserved.
Now, the interesting question is, if we move a test charge in an electric field from point A to point B, does the change in electric potential energy depend on the path we take from A to B? That is to say, does the amount of work needed to move a charge between two points depend on the route we take?
The answer, in electrostatics, is no. Regardless of whatever winding route we take from A to B, the amount of work is the same, and hence the change in electric potential energy will be the same. This means that the electrostatic force is a conservative force, and the electric field is a conservative field. Gravitational force is another example of a conservative force. An example of a non-conservative force is friction - the energy lost to friction does depend on the path. This means we can uniquely define the electrostatic energy that \(q_0\) has just based on its position in space.
If we have a fixed charge, \(q\), and we bring in a charge \(q_0\) from infinity to a distance of \(r\), then the total electric potential energy of the system is given by:
\[U = \frac{1}{4\pi \epsilon_0} \frac{qq_0}{|r|} = k \frac{qq_0}{|r|}\]
Several things to note:
Electric potential energy is a scaler - it has no direction. While this make the maths far easier, it is also a big source of confusion!
Electric potential energy falls off as \(1/|r|\) not \(1/r^2\). Also a source of confusion.
Electric potential energy has SI units of Joules, J.
Electric potential energy can be positive or negative. If the two charges are of opposite sign, then it will be negative. This is because opposite charges are attracted to each other. So the most possible electric potential energy is when they are infinitely far apart, and as the test charge approaches it loses potential energy.
Just like gravitational potential energy, the absolute value of electrical potential energy doesn’t mean anything physically, it is only the change in the electric potential energy which matters. So we are free to add a constant without changing anything. This also means that we are free to define the point at which there is zero potential energy anywhere we like.
Consider a charge, \(q\), which is generating an electric field, and a second test charge, \(q_0\) which we will move. If an infinitesimal force \(d\vec{F_W}\) is applied to move \(q_0\) an infinitesimal distance \(d \vec{dl}\), then the work done is \[dW = d\vec{F_W}.d\vec{l}\]
In moving \(q_0\) from point A to point B, the work done is given by: \[W = \int_A^B\vec{F_W}.d\vec{l}\]
where \(\vec{F}\) is the force applied. In order to move the charge without giving it a resultant velocity, the force applied would need to be equal and opposite to the electrostatic force, \(F\), i.e. \[\Delta U = - \int_A^B \vec{F}.d\vec{l}\]
This tells us the difference in potential energy between two points. It is only ever really the difference in energy we care about, that is the only thing that has a physical meaning. If we want to specify the absolute potential energy, rather than a difference, we need to choose some reference point at which we will say the electric potential energy is zero (just like how me might choose the surface of the Earth as the point with zero gravitational potential energy). We are free to choose this wherever we like. By convention we choose this point as a point which is infinitely far away from the charge \(q\). This turns out to be convenient because infinitely far away from a charge, the force and the electric field from that charge goes to zero.
The force, \(F\), at a distance \(r\) is given by Coulomb’s Law \[\vec{F} = \frac{kqq_0}{r^2} \hat{r}\]
and so to find out the potential energy for \(q_0\) at a distance \(r\) from this charge, we need to imagine bringing in \(q_0\) from infinity (i.e. we calculate the difference in energy from this point with infinity). So we need to integrate from \(\infty\) to \(r\): \[U = - \int_{\infty}^r \vec{F}.d\vec{l} = - \int_{\infty}^r\frac{kqq_0}{r^2} \hat{r}.d\vec{l}\]
Now, \(\hat{r}.d\vec{l}\) (a dot product) is simply \(dr\). So we have: \[\begin{aligned} U &= - \int_{\infty}^r \frac{kqq_0}{r^2} dr \\ &= - \bigg[ -\frac{kqq_0}{r} \bigg| _{\infty}^r \bigg] \\ &= k\frac{qq_0}{r} \end{aligned}\]
which is our definition of electric potential energy.
The electric potential, \(V\), at a point is the electric potential energy a charge of 1 C would have were it at that point. Like the electric field, the electric potential is a field, it has a value everywhere in space. The electric potential is a scalar field, and not a vector, and so we sometimes call it the scalar potential.
The units of potential are Joules per Coulomb, J/C. Differences in potential between two points, the potential difference, is sometimes known as a voltage, and we then call this unit Volts, V. This is an important concept in electrical circuits which you will learn about later in PH322.
Using our definition of electric potential energy, and recalling \(\vec{F} = q_0\vec{E}\), we have \[\Delta V = \frac{\Delta U}{q_0} = - \int_A^B \vec{E}.d\vec{l}\]
As for electric potential energy, it is only the difference in potential that matters, not the absolute value. So we are free to define zero potential at any place we like. By convention we say the potential is 0 at a point infinitely far away from the charge. So when we talk about the potential at a point, this is really the potential difference between that point and a point at infinity. So by analogy with the derivation for electric potential energy, we can define the electric potential at a distance \(r\) from a point, known as the Coulomb potential:
\[V = \frac{1}{4 \pi \epsilon_0} \frac{q}{|r|} = k \frac{q}{|r|}\] Note that \(|r|\) is the magnitude of the distance, i.e. \(|r| = |\vec{r}|\).
If we know the potential, then the electric field can be calculated from:
\[\vec{E} = -\nabla V = - \frac{\partial V}{\partial x} \hat{i} - \frac{\partial V}{\partial y} \hat{j} - \frac{\partial V}{\partial z} \hat{k}\] where \(\hat{i}\), \(\hat{j}\), and \(\hat{k}\) are units vectors in the x, y and z directions, respectively.
That is to say, the electric field pointing in any direction is the derivative of the electric potential in that direction. This is possible because, as we have said, electric field is a conservative vector field. Mathematically, the meaning of a conservative vector field is that it can be expressed as the gradient of a scalar field. In the case of the electric field, this scalar field is the scalar potential.
See Tipler/Mosca Examples 23-1 to 23-5, 23-7.
So, what does the potential actually mean? We can think of the electrical potential at a point as the electrical potential energy that a charge of 1C would have if it was sitting at that point. Or, more strictly, it is the potential energy shared between the charge creating the potential and this 1C test charge. However, just like how the electric field has a meaning even when there is no test charge to feel the electric force, the potential still has a meaning even when there isn’t a charge to have the potential energy.
A difference from gravitational potential is that the electric potential can either increase or decrease as we approach the source of the field, depending on whether the source is positive or negative.
If the source of the field is a positive charge, then a positive test charge is repelled. We have to do work to push the test charge towards the source charge, and so it gains potential (just like a mass gains potential energy if we do work to push it uphill.) If we are using the convention that the potential at infinity is zero, then the potential will be positive.
If the source of the field is a negative charge, then a positive test charge is attracted. The test charges loses potential (just like a mass loses potential energy as it rolls down a hill.) If we are using the convention that the potential at infinity is zero, then the potential will be negative.
Non-examinable Aside: You might notice that the electric potential, being a scalar, gives us only one ‘number’ for each point in space, while the electric field, being a vector, gives us three ‘numbers’. So how is it that the electric field can be calculated from the electric potential, where does this extra information come from? In turns out that, in electrostatics, one cannot simply have any electric field distribution, there are only certain allowed electric fields which allow us to define the electric potential in this way. That is to say. if we simply chose our \(E_x\), \(E_y\) and \(E_z\) at random, this would almost certainly not be a conservative field. To put it another way it is not possible to create any arbitrary electric field distribution using only static charges. Only conservative fields are created from static charges, so we don’t have to worry about this in PH322. It turns out that when we have a moving electric charges, or magnetic fields, then the fields are not conservative, and can’t be described just by a scalar potential - there is also a vector potential. In later courses you will learn about this, and understand how it is encoded in Maxwell’s Equations.
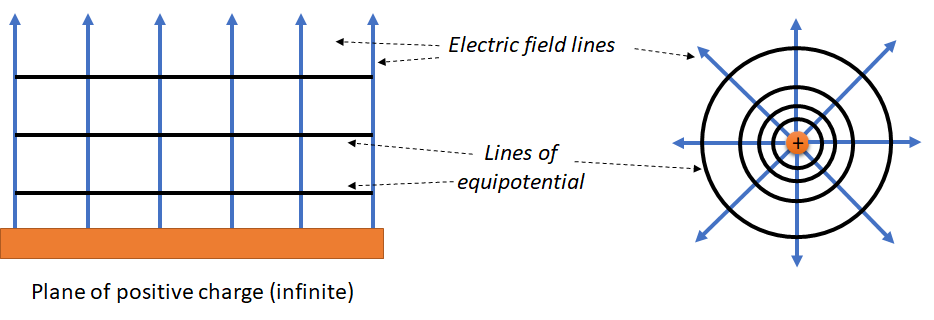
If we connect up points of equal potential, we get lines of equipotential. These are somewhat analogous to contour lines on a map, which join up points of equal altitude. If we move a charged particle along a line of equipotential, it stays at the same potential. So it does not gain or lose energy. Examples are shown in Figure 3.1. There is an interesting relationship between electric field lines and lines of equipotential. Field lines are always perpendicular to lines of equipotential. So, if we go back to our contour lines on a map analogy, electric field lines always point directly downhill. This will be obvious once you have studied the meaning of the gradient of a scalar field in PH312, it always points along the steepest slope of the field, i.e. the direction of the electric field vector.

Potential obeys the super-position principle (which is unsurprising if we think how it is related to the electric field). So the potential from a collection of point charges is the sum of the potential from each charge, and the potential from a continuous charge distribution is the integral over the distribution. Some care is needed, remember that the \(r\) in the denominator is the absolute value of the distance, it is not directional.
Because electric potential obeys the super-position principle, we can also sum the potential due to a collection of discrete charges or integrate over a continuous charge distribution. This is actually easier than for the electric field because potential is a scalar rather than a vector.
Consider a rod of uniform charge density \(l\) and length \(L\). What is the electric potential a distance \(d\) from the end of the rod, along the axis?
An element of length \(dx\) has charge \(dq = ldx\). The electric potential from this element, \(dV\), is given by: \[dV = \frac{kdq}{x+d}\] where \(x\) is the position of the element along the rod and hence \(x+d\) is the distance to the point where we are calculating the potential. The potential is therefore: \[\begin{aligned} V &= k \lambda \int_0^L \frac{dx}{x+d} \\ &= k \lambda [\ln(x+d)]_{x=0}^{L} \\ &= k \lambda [\ln (L +d) - \ln d] \\ &= k \lambda \ln \frac{L+d}{d} \end{aligned}\]
Note that when we are far from the rod, \(L << D\), then: \[V = k \lambda \ln [1+L/d] \approx k \lambda L/d = kQ/d\]
at which point it looks like a point charge.
Consider a rod of uniform charge density \(\lambda\) and length \(L\). What is the electric potential a
distance \(d\) from the rod,
perpendicular to the rod?
As before, an element of length \(dx\)
has charge \(dq = \lambda dx\), giving
rise to a potential of \(dV = k\lambda
dx/r\), where \(r\) is the
magnitude of the distance from the element to the point where we are
calculating the potential. From geometry, \(r
= \sqrt{x^2 + d^2}\), and so, if we label the two ends of the rod
as \(a\) and \(b\), then the electric potential is given
by:
\[\begin{aligned} V &= k \lambda \int_a^b \frac{dx}{r} \\ &= k \lambda \int_a^b \frac{dx}{\sqrt{x^2 + d^2}} \\ &= k \lambda [\ln \sqrt{x^2 + d^2} + x]_{x=a}^b \\ &= k \lambda \ln \bigg [ \frac{\sqrt{b^2 + d^2} + b} {\sqrt{a^2 + d^2} + a} \bigg] \end{aligned}\]
In Section 2.5.5 we calculated the electric field from an infinite plane of charge to be \(2k\epsilon_0\). This doesn’t depend on distance, \(r\), i.e. the electric field is the same everywhere. This is a problem if we now try to calculate the potential since we want the integral: \[V = \int_{-\infty}^{r}E.d\vec{r}\]
which is unfortunately infinite.
This problems arises because of the way we chose our zero reference. This is infinitely far away, but because normally the electric field drops rapidly with distance and hence goes to zero at infinity, the line integral over the field from infinity to our point of interest is finite. But for the extreme case of an infinite plane of charge, the electric field at infinity is still \(2k\epsilon_0\).
In reality of course we never have an infinite plane of charge. If we get far enough way from any finite plane of charge then it will start to look like a point, the electric field will drop off as \(1/r^2\) and the integral will become finite again. So this is not a real problem, it arises only because the approximation we chose to use, that a finite plane of charge looks like an infinite plane of charge when you are very close up, is a very bad approximation once you get very far away.
Note also that we can still work out the potential difference between two points in the field from an infinite plane of charge, the line integral between any two points is finite. It’s just that it no longer makes sense to choose a point an infinity as our reference 0 potential, because the field at infinity no longer goes to zero.