Section 2 - Electric Field

Using Coulomb’s law, and the superposition principle, we can now calculate the force from any distribution of charges. (At least in principle, if we can do the integral!) However, we will see that in many cases it makes sense to define something called an electric field. The electric field is an example of a vector field.

Vector Fields

You are familiar with the idea of scalars and vectors. A scalar quantity has only magnitude, examples are temperature and mass. A vector quantity has both magnitude and direction, examples are velocity and force.

A scalar field means that for each point in space, we have a number. An example from everyday experience would be the temperature on a weather map. At each point, we define a single number, which is the temperature at that point. While a weather map might only show the temperatures at a few points, in principle this field is continuous, we can specify the temperature at points arbitrarily finely.

A vector field has a magnitude and a direction for each point in space. The corresponding example of a vector field is the wind map. Here the map shows the strength of the wind (the magnitude of the wind vector) but also its direction. This is usually done using arrows, with the length of the arrow telling us the strength of the wind at the point at the start of the arrow, and the direction of the arrow telling us the direction of the wind at that point. Again, while we can only draw arrows at a limited number of places (to stop them being on top of each other), the wind speed and direction can be defined everywhere.
Non-examinable Aside - You might wonder whether the electric field is a real physical ‘thing’. After all, can’t we just think in terms of forces between charges - if there is no charge present to feel a force due to the electric field, then does the field have any residual meaning? In electrostatics, where we have electric fields due to eternal, non-moving electric charges, this is a reasonable arguments, but in later courses where you study electrodynamics, and find electric fields hanging around long after the charges which created them have left the shop, we find it really does make more sense to think in terms of fields.

Definition of Electric Field

The electric field can be thought of as the electrical force which would be experienced by a 1C charge (although it is really more fundamental than this rather pedestrian definition). Hence:

The magnitude of the electric field a distance \(r\) from a point charge of \(q\) is given by: \[E=\frac{1}{4\pi\epsilon_0}\frac{q}{r^2}\] As for the electric force, this is really a vector quantity: \[\vec{E}=\frac{1}{4\pi\epsilon_0}\frac{q}{r^2}\hat{r}\] where \(r\) is a unit vector pointing from the charge \(q\) to the point where we are determining the electric field. The force, \(\vec{F}\), on a charge, \(q_0\), placed at this point is then: \[\vec{F}=q_0\vec{E}\]

Motion in an Electric Field

A particle of charge \(q\) experiences a force of \(q\vec{E}\). From \(F=ma\), this tells us that if that particle has a mass of \(m\), it will experience an acceleration of: \[\vec{a} = \frac{q}{m}\vec{E}\]

This allows the charge-to-mass ratio of the particle in a known electric field to be determined by measuring its acceleration. There is a classic experiment, first performed by J.J.Thompsin in 1897, in which the charge to mass ratio of electrons is calculated, although to do this correctly is is also necessary to make some relativistic corrections.

Superposition Principle for Electric Field

Since \(\vec{F}=q_0\vec{E}\), the superposition principle also holds for electric field. Hence:

The total electric field due to a collection of \(N\) point charges of charge \(q_i\) is given by: \[\vec{E} = \frac{1}{4\pi\epsilon_0}\sum_{i=1}^{N} \frac{q_i}{r_i^2} \hat{r_i} = k\sum_{i=1}^{N} \frac{q_i}{r_i^2} \hat{r_i}\]

where \(\hat{r_i}\) is the unit vector pointing from the \(i\)th charge (\(q_i\)) to the point where we calculate the field, and \(r_i\) is the distance between \(q_i\) and the point where we calculate the field.

Electric Field Lines

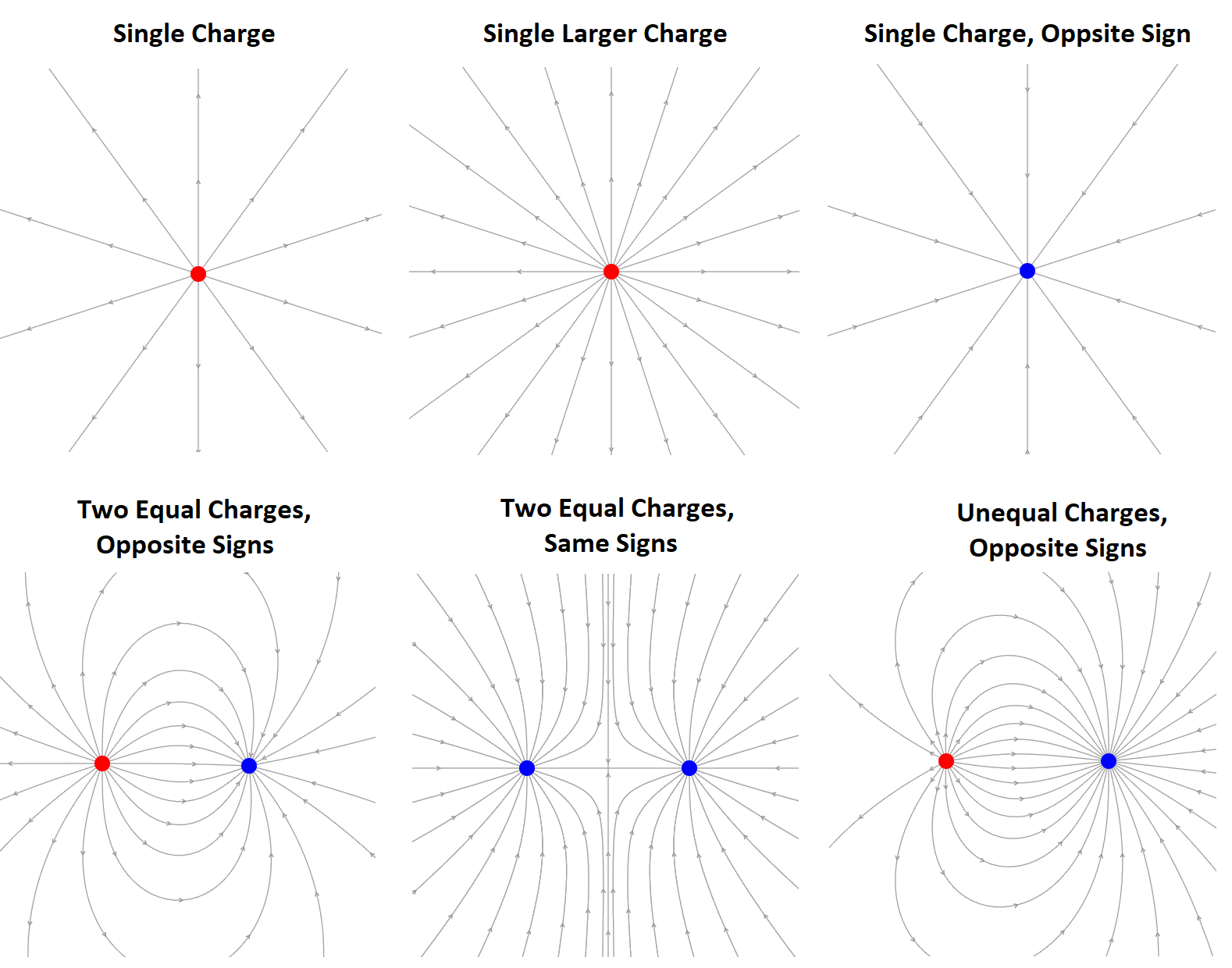
Electric field lines are a way of representing an electric field visually. Recall that an electric field is a vector field, so we need to represent both the amplitude and the direction at different points in space. One way to represent an electric field might be to draw lots of different arrows, with the direction the arrow is pointing representing the direction of the field, and the length of the arrow the strength of the field. The electric field is defined everywhere in space, and so to represent it fully we would need arrows starting everywhere, but of course then they would overlap and we would just have a black box, which wouldn’t tell us very much. So we can only represent the field at some discrete points. Incidentally, this is exactly how the vector field of wind is often represented on a weather map.

However, this is not the way we normally represent electric fields. Instead we use field lines. You can imagine a field line as being what you get when you join up a line of arrows. Once we do this we can no longer tell how long the arrows were and hence how strong the field is. Instead, we use the density of the lines to tell us the field strength. Examples are shown in Figure 1. When drawing field lines we observe the following rules: